Question 503508: If I have the following numbers:
2,6,12,20,30,42...
I can see the relationship between the numbers:
+4 +6 +8 +10 +12
+2 +2 +2 +2
What kind of sequence is this? (arithmetic/geometric etc)
Thank you!
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The two main types of series/sequences are 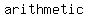 and and 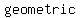 . Some sequences are . Some sequences are 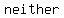 of these. of these.
Itís important to be able to identify what type of sequence is being dealt with.
And 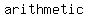 series is one where series is one where  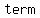 is equal the one before it is equal the one before it   number. For example: 5, 10, 15, 20, Ö Each term in this sequence equals the term before it with number. For example: 5, 10, 15, 20, Ö Each term in this sequence equals the term before it with  added on. added on.
In contrast, a 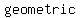 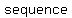 is one where each term equals the one before it is one where each term equals the one before it 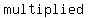 by a by a 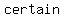 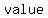 . An example would be 3, 6, 12, 24, 48, Ö Each term is equal to the prior one multiplied by . An example would be 3, 6, 12, 24, 48, Ö Each term is equal to the prior one multiplied by  . .
so, it's 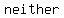 of these of these
|
|
|