Here is a geometric series:
2 + 6 + 18 + 54 + 162 + 486
A. It has 6 terms. So we say 
B. It has first term 2. So we say 
C. It has common ratio 3. So we say 
D. It has sum 728. So we say 
The reason we say it has common ratio 3 is because:
1. The 2nd term 6 divided by the 1st term 2 is 3.
2. The 3rd term 18 divided by the 2nd term 6 is 3.
3. The 4th term 54 divided by the 3rd term 18 is 3.
4. The 5th term 162 divided by the 4th term 54 is 3.
5. The 6th term 486 divided by the 5th term 162 is 3.
Since all those divisions come out 3, it is a geometric
series, with common ratio 3.
The formula for the sum 
of any FINITE geometric series is:
So in the above case, substituting:
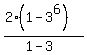
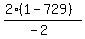
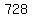We can also find just by adding:
2
6
18
54
162
486
728
But if there were 100 terms instead of just 6 that would
take too long, but the formula would be much shorter.
-----------------------------------
There are also INFINITE geometric series that never end, but goes
on forever and ever. That is when r < 1, like this:
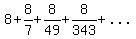A. It has infinitely many terms terms.
B. It has first term 8. So we say 
C. It has common ratio 
. So we say 
We could never add them all up since the terms go on forever.
However there is a number that we get closer and closer to as
we add more and more terms.
So we say that the sum of all "infinity" of those terms is given by
this formula:
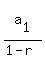
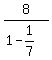
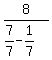
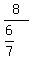
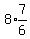
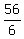
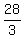So the more terms we add, the closer to 28/3 we will get.
28/3 is the decimal 9.333333333...
Notice that when we add just the first 4 terms we get 9.329446064
which is well on the way to 9.333333333...
Hope this helps you.
Edwin
