Question 389734: write a recursive formula for the sequence 15, 26, 48, 92, 180,... Then find the next term
Found 2 solutions by richard1234, Edwin McCravy:
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Note that the difference between two consecutive terms 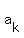 and and 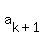 is an increasing geometric sequence. In general, we have the sequence: is an increasing geometric sequence. In general, we have the sequence:



 , etc. , etc.
It is seen that  for all for all  . We can substitute p = 11 and r = 2 to obtain , . We can substitute p = 11 and r = 2 to obtain ,
 where where 
Since  , , 
Note that a recursive sequence is defined on previous terms. It is possible to write each expression 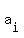 in terms of i and other constants, but it wouldn't be recursive. Using the sum of a geometric sequence, we can get in terms of i and other constants, but it wouldn't be recursive. Using the sum of a geometric sequence, we can get

Checking, we have  , ,  , ,  ,etc. which is the same sequence as the recursion. ,etc. which is the same sequence as the recursion.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor found a GENERAL formula, not a RECURSIVE formula.
List those in a column beside the numbers n=1 through n=5
n an
1 15
2 26
3 48
4 92
5 180
Out beside each number, write the difference between it
and the number just below it.
n an
1 15 11
2 26 22
3 48 44
4 92 88
5 180
Observe that those differences are all multiples of 11
n an
1 15 11 = 1×11
2 26 22 = 2×11
3 48 44 = 4×11
4 92 88 = 8×11
5 180
Next we observe that the numbers 1,2,4,8 are these powers of 2:
20,21,22,23
n an
1 15 11 = 1×11 = 20×11
2 26 22 = 2×11 = 21×11
3 48 44 = 4×11 = 22×11
4 92 88 = 8×11 = 23×11
5 180
Finally we observe that the exponents of 2 are 1 less than the
values on n in the left-most column, and 1 less than n is n-1.
So we think this way : To get the next term an+1 from the
previous term an we must add 2n-1×11.
So the recursion formula is
a1 = 15, an+1 = an + 2n-1×11
So to get the 6th term, a6, from the 5th term, a5,
we substitute 5 for n in an+1 = an + 2n-1×11
a5+1 = a5 + 25-1×11
a6 = a5 + 24×11
Now we substitute 180 for a5
a6 = 180 + 24×11
a6 = 180 + 16×11
a6 = 180 + 176
a6 = 356
Edwin
|
|
|