SOLUTION: Missy made her annual income of RM25,710 in the fourth year and RM38,560 in the ninth year working in SIMEC Ltd. Assuming that her annual income behave like an arithmethic sequence

Algebra ->  Sequences-and-series -> SOLUTION: Missy made her annual income of RM25,710 in the fourth year and RM38,560 in the ninth year working in SIMEC Ltd. Assuming that her annual income behave like an arithmethic sequence      Log On


   

Question 325534: Missy made her annual income of RM25,710 in the fourth year and RM38,560 in the ninth year working in SIMEC Ltd. Assuming that her annual income behave like an arithmethic sequence:
a. How much was her annual income in the first year
Found 2 solutions by info@email-tutors.com, MathTherapy:
Answer by info@email-tutors.com(9) About Me  (Show Source):
You can put this solution on YOUR website!
An arithemetic sequence is an additive one. This means that each year an unknown amount "x" is added to each sequence. Between the 4th and 9th years, there are 5 sequences. Also, between the 4th and 9th years, there are 12850 RM.
12850 / 5 = 2570 RM per year. Between the fourth and ninth years, you add 2570 to each year. Between the first and fourth years, you subtract 2570 to each year (you are going backwards, so it requires subtraction instead of division).
therefore, the third year would be 38560 - 2570
the second year would be: 38560 - (2*2570)
The first year would be: 38560 - (3 * 2570) = 30850 RM
That is the answer. We hope that we have been of help. Should you require any additional information, please feel free to contact us via our profile.
Sincerely,
The Email Tutors Team
www.email-tutors.com

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Missy made her annual income of RM25,710 in the fourth year and RM38,560 in the ninth year working in SIMEC Ltd. Assuming that her annual income behave like an arithmethic sequence:
a. How much was her annual income in the first year

Since this is an arithmetic sequence, we can determine the difference between the years by subtracting year 4's amount from year 9's amount, and then divide this amount by 5 (the difference between the years), or,

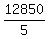%2838560+-+25710%29%2F5 = 12850%2F5 = $2,570

Since year 1 to year 4 covers 3 years, we multiply $2,570 by 3 and subtract this result from year 4's amount. This gives us: $25,710 - $7,710 = $18,000.

This means that her annual income in the first year was: $highlight_green%2818000%29.

This first year annual income could have also been found using the arithmetic progression formula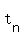, t%5Bn%5D+=+t%5B1%5D+%2B+%28n+-+1%29d, where t%5Bn%5D is the term, "n" is the term number, t%5B1%5D is the first term, and d is the common difference.