SOLUTION: Evaluate the product of the following fractions: {{{((1/2 -1/3) / (1/3-1/4))}}}{{{"×"}}}{{{((1/4 - 1/5)/(1/5-1/6))}}}{{{"×"}}}{{{((1/6-1/7)/(1/7-1/8))}}}{{{"×"}}}{{{"···"}}}{{{"×"

Algebra ->  Sequences-and-series -> SOLUTION: Evaluate the product of the following fractions: {{{((1/2 -1/3) / (1/3-1/4))}}}{{{"×"}}}{{{((1/4 - 1/5)/(1/5-1/6))}}}{{{"×"}}}{{{((1/6-1/7)/(1/7-1/8))}}}{{{"×"}}}{{{"···"}}}{{{"×"      Log On


   

Question 315720: Evaluate the product of the following fractions:
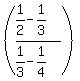
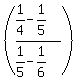
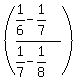
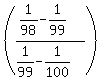
%28%281%2F2+-1%2F3%29+%2F+%281%2F3-1%2F4%29%29%22%D7%22%28%281%2F4+-+1%2F5%29%2F%281%2F5-1%2F6%29%29%22%D7%22%28%281%2F6-1%2F7%29%2F%281%2F7-1%2F8%29%29%22%D7%22%22%B7%B7%B7%22%22%D7%22%28%281%2F98-1%2F99%29%2F%281%2F99-1%2F100%29%29

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
%28%281%2F2+-1%2F3%29+%2F+%281%2F3-1%2F4%29%29%22%D7%22%28%281%2F4+-+1%2F5%29%2F%281%2F5-1%2F6%29%29%22%D7%22%28%281%2F6-1%2F7%29%2F%281%2F7-1%2F8%29%29%22%D7%22%22%B7%B7%B7%22%22%D7%22%28%281%2F98-1%2F99%29%2F%281%2F99-1%2F100%29%29


The sequence of upper left denominators is 2,4,6,8,···,98, and the
general term for those upper left denominators is 2n, where n goes 
from 1 to 49. 

Therefore the general factor of the whole product is 

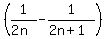
%281%2F%282n%29-1%2F%282n%2B1%29%29%2F%281%2F%282n%2B2%29-1%2F%282n%2B3%29%29 where n goes from 1 to 49

Simplifying this general factor:

%281%2F%282n%29-1%2F%282n%2B1%29%29%2F%281%2F%282n%2B2%29-1%2F%282n%2B3%29%29=%22%22

%281%2F%282n%29-1%2F%282n%2B1%29%29%22%F7%22%281%2F%282n%2B2%29-1%2F%282n%2B3%29%29=%22%22

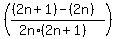
%28%28+%282n%2B1%29-%282n%29+%29%2F%282n%2A%282n%2B1%29%29%29%22%F7%22%28+%28%282n%2B3%29-%282n%2B2%29+%29%2F%28%282n%2B2%29%282n%2B3%29%29%29=%22%22

%28%28+2n%2B1-2n+%29%2F%282n%2A%282n%2B1%29%29%29%22%F7%22%28+%282n%2B3-2n-2+%29%2F%28%282n%2B2%29%282n%2B3%29%29%29=%22%22

%28+1+%2F%282n%2A%282n%2B1%29%29%29%22%F7%22%28+1+%2F%28%282n%2B2%29%282n%2B3%29%29%29=%22%22

%28+1+%2F%282n%2A%282n%2B1%29%29%29%22%D7%22%28+%28%282n%2B2%29%282n%2B3%29%29%2F1%29=%22%22

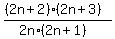%28+%282n%2B2%29%282n%2B3%29+%29%2F%282n%2A%282n%2B1%29%29, where n goes from 1 to 49.

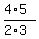Substituting in n=1, %284%2A5%29%2F%282%2A3%29
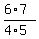Substituting in n=2, %286%2A7%29%2F%284%2A5%29
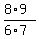Substituting in n=3, %288%2A9%29%2F%286%2A7%29
···
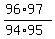Substituting in n=47, %2896%2A97%29%2F%2894%2A95%29
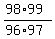Substituting in n=48, %2898%2A99%29%2F%2896%2A97%29
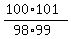Substituting in n=49, %28100%2A101%29%2F%2898%2A99%29

So we have:

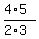
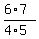
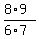
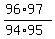
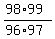
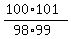
%284%2A5%29%2F%282%2A3%29%22%D7%22%286%2A7%29%2F%284%2A5%29%22%D7%22%288%2A9%29%2F%286%2A7%29%22%D7%22%22%B7%B7%B7%22%22%D7%22%2896%2A97%29%2F%2894%2A95%29%22%D7%22%2898%2A99%29%2F%2896%2A97%29%22%D7%22%28100%2A101%29%2F%2898%2A99%29

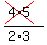
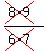
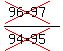
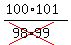%28cross%284%2A5%29%29%2F%282%2A3%29%22%D7%22%28cross%286%2A7%29%29%2F%28cross%284%2A5%29%29%22%D7%22%28cross%288%2A9%29%29%2F%28cross%286%2A7%29%29%22%D7%22%22%B7%B7%B7%22%22%D7%22%28cross%2896%2A97%29%29%2F%28cross%2894%2A95%29%29%22%D7%22%28cross%2898%2A99%29%29%2F%28cross%2896%2A97%29%29%22%D7%22%28100%2A101%29%2F%28cross%2898%2A99%29%29

As we see every numerator cancels with the denominator of the next factor,
except in the last, or 49th, factor where there is no next factor.  And every
denominator gets canceled with the preceding numerator except the 1st factor
where there is no preceding factor.  Thus the product becomes:

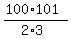
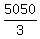%28100%2A101%29%2F%282%2A3%29%22=%225050%2F3

Edwin