SOLUTION: The first difference of a sequence is 6, 10,14,18. The sum of the first two terms of the original sequence is 24. Find the first three term of the original sequence. the first term

Algebra ->  Sequences-and-series -> SOLUTION: The first difference of a sequence is 6, 10,14,18. The sum of the first two terms of the original sequence is 24. Find the first three term of the original sequence. the first term      Log On


   

Question 312694: The first difference of a sequence is 6, 10,14,18. The sum of the first two terms of the original sequence is 24. Find the first three term of the original sequence. the first term of the original sequence is?
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
If you look at the second differences, you'll notice they are the same,
%2810-6%29=4
%2814-10%29=4
%2818-14%29=4
so the generating formula is a quadratic function,
T%28n%29=an%5E2%2Bbn%2Bc
Generate the first couple of terms
First term: 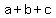n=1, a%2Bb%2Bc
Second term: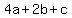n=2, 4a%2B2b%2Bc
Third term: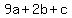n=3,9a%2B2b%2Bc
Fourth term:n=4,16a%2B4b%2Bc
.
.
.
Use the first differences to solve for a and b.
First difference :4a%2B2b%2Bc-a-b-c=6
1.3a%2Bb=6
Second difference:9a%2B3b%2Bc-4a-2b-c=10
2.5a%2Bb=10
Subtracting eq. 1 from eq. 2,
5a%2Bb-3a-b=10-6
2a=4
a=2
Then from eq. 1,
3a%2Bb=6
6%2Bb=6
b=0
Then using the first two terms, solve for c.
a%2Bb%2Bc%2B4a%2B2b%2Bc=24
2%2B0%2Bc%2B8%2B0%2Bc=24
10%2B2c=24
2c=14
c=7
So the generating formula is,
T%28n%29=2n%5E2%2B7
highlight%28+T%281%29=9%29
highlight%28+T%282%29=15%29
highlight%28+T%283%29=25%29
T%284%29=39
T%285%29=57
and you can verify that the first differences are correct.