Question 283866: Explain how the common ratio for a geometric sequence with positive terms determines whether the terms increase or decrease.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! A geometric sequence is a sequence of the form
 , , 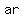 , , 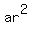 , , 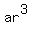 , .... , ....
where 'a' is the starting term and 'r' is the common ratio. If 'a' is positive, then the value of 'r' will determine whether the terms will increase or decrease. If 'r' is greater than 1 (ie 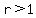 ), then the terms will increase, while on the other hand, if 'r' is less than 1 ( ), then the terms will increase, while on the other hand, if 'r' is less than 1 ( ), then the terms will decrease. Finally, if 'r' is equal to 1, then the terms will remain the same. ), then the terms will decrease. Finally, if 'r' is equal to 1, then the terms will remain the same.
If 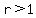 , then we can write 'r' as , then we can write 'r' as  where where 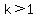 . Plug this into the sequence above to get: . Plug this into the sequence above to get:
 , , 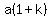 , , 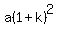 , , 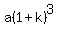 , .... , ....
Now expand and distribute
 , ,  , , 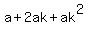 , , 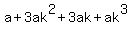 , .... , ....
Notice how the second term  is bigger than 'a' since 'ak' is positive ('a' is positive and so is 'k'). Symbolically, this can be proven by showing that is bigger than 'a' since 'ak' is positive ('a' is positive and so is 'k'). Symbolically, this can be proven by showing that 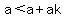 simplifies to simplifies to 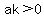 (which is true, as shown above). Similar arguments can be made to show that (which is true, as shown above). Similar arguments can be made to show that 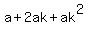 is bigger than is bigger than  . Similarly, we can show that . Similarly, we can show that 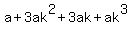 is greater than is greater than 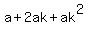 , and so on. , and so on.
For  , we can write 'r' as , we can write 'r' as  where where 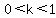 (we want to keep 'r' positive). I'll let you plug in (we want to keep 'r' positive). I'll let you plug in 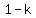 for 'r'. Use similar arguments shown above to show that each term will get smaller. for 'r'. Use similar arguments shown above to show that each term will get smaller.
Note: if  , then the sequence , then the sequence
 , , 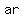 , , 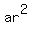 , , 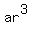 , .... , ....
becomes
 , , 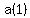 , , 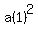 , , 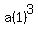 , .... , ....
which simplifies to
 , ,  , ,  , ,  , .... , ....
|
|
|