The perimeter of a triangle is 15. The lengths of the sides are integers. If the length of one side is 6, what is the shortest possible length of another side of the triangle?
Suppose the sides are a, b, and 6. Then

 By the three triangular inequalities:
By the three triangular inequalities:
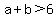 ,
, 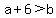 ,
, 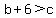 Since
Since  ,
,  Substituting in the three triangular inequalities:
Substituting in the three triangular inequalities:
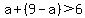 ,
, 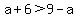 ,
, 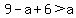
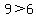 ,
,  ,
, 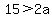 From
From  we have
we have
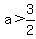 , or
, or 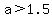 , and since a is an integer,
{a>=2}}}
So 2 is the smallest integer a can be.
From
, and since a is an integer,
{a>=2}}}
So 2 is the smallest integer a can be.
From 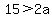 , we can also similarly show that 7 is the largest
integer a can be.
We could have interchanged a and b and shown the same for b, so
the smallest integer either of the sides other than the side that is 6
coul dbe is 2.
Edwin
, we can also similarly show that 7 is the largest
integer a can be.
We could have interchanged a and b and shown the same for b, so
the smallest integer either of the sides other than the side that is 6
coul dbe is 2.
Edwin