SOLUTION: three numbers are in AP and their sum is 21. if 1,5,15 are added to them respectively,they form a GP.The numbers are. please tell me the solution and method of solving this type o

Algebra ->  Sequences-and-series -> SOLUTION: three numbers are in AP and their sum is 21. if 1,5,15 are added to them respectively,they form a GP.The numbers are. please tell me the solution and method of solving this type o      Log On


   

Question 259658: three numbers are in AP and their sum is 21. if 1,5,15 are added to them respectively,they form a GP.The numbers are.
please tell me the solution and method of solving this type of questions using this formula for Ap:(a-d),a, (a+d) and for GP:a/r,a,ar
the option for the above question is :A)5,7,9 B)9,7,5 C) none of these
the above is question of AP and GP.
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
Let A be your starting number, d be the difference for the arithmetic progression.
A%2B%28A%2Bd%29%2B%28A%2Bd%2Bd%29=21
3A%2B3d=21
A%2Bd=7
Then from the geometric progression information,
First: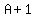A%2B1
Second: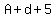A%2Bd%2B5
Third:A%2Bd%2Bd%2B15=A%2B2d%2B15
Since they are in geometric progression, each successive pair equals the common ratio.
%28A%2Bd%2B5%29%2F%28A%2B1%29=%28A%2B2d%2B15%29%2F%28A%2Bd%2B5%29
From eq. 1, you know,
A%2Bd=7
Substitute,
%28A%2Bd%2B5%29%2F%28A%2B1%29=%28A%2B2d%2B15%29%2F%28A%2Bd%2B5%29
%287%2B5%29%2F%28A%2B1%29=%287%2Bd%2B15%29%2F%287%2B5%29
12%2F%28A%2B1%29=%2822%2Bd%29%2F12
%28A%2B1%29%2822%2Bd%29=144
Again using eq. 1,
A%2Bd=7
d=7-A
%28A%2B1%29%2822%2Bd%29=144
%28A%2B1%29%2822%2B7-A%29=144
%28A%2B1%29%2829-A%29=144
29A-A%5E2%2B29-A=144
-A%5E2%2B28A%2B29=144
-A%5E2%2B28A-115=0
A%5E2-28A%2B115=0
You can factor,
%28A-23%29%28A-5%29=0
Two solutions:
A-23=0
A=23
d=7-A
d=7-23=-16
.
.
.
A-5=0
A=5
d=7-A
d=7-5=2
.
.
.
A) (5,7,9) is one solution.
But (23, 7, -9) is also a solution.