Question 25541: I have an assignment due on arithmetic series of numbers. I have been studying my book and can't seem to figure out what I am supposed to do to make or solve the equations. Is there anyway you can help? Thank you in advance.
Use the arithmetic series of numbers 1,3,5,7,9,...to find the following:
What is d, the difference between any 2 numbers?
Using the formula for the nth term of an arithmetic series, what is 101st term?
Using the formula for the sum of an arithmetic series, what is the sum of the first 20 terms?
Using the formula for the sum of an arithmetic series, what is the sum of the first 30 terms?
What observation can you make about these sums of this series(HINT: It would be beneficial to find a few more sums like the sum of the first 2, then the first 3 etc.)?
I know it seems like a lot but it really is just one problem broken down into several sections. I have no idea how to so this so I would be VERY thankful for any help you can give me.
Found 2 solutions by askmemath, vanetiks:
Answer by askmemath(368)   (Show Source):
You can put this solution on YOUR website! "d" is the common difference between any 2 consecutive numbers
In this case the sequence is 1,3,5,7........
So the difference becomes 3-1= 5-3 = 7-5 = 2
Now every arithmetic series is represented by 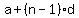 where a is the first term and d the common difference
n-1 is the nth term
For the given series, a = 1 since the series begins with 1 and d = 2
The 1st term is 1
2nd term is 3
So the 101st term becomes 1+(101-1)2 = 1+200 = 201
Sum to n terms is given by 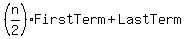 where n is the number of terms.
Please solve this on your own as I have already shown you above how to find the last term. Again you can the find the sum to the first 30 terms with the same formula.
Adding the first two numbers or the first three or so on, you will find that the sum is always an Even Number.
Answer by vanetiks(6) (Show Source):
You can put this solution on YOUR website! Using the formula for the nth term of an arithmetic sequence, what is 101st term? Answer: 201
Show work in this space.
fn = 2n - 1
f101 = 2*101-1 = 201
Using the formula for the sum of an arithmetic series, what is the sum of the first 20 terms?
Answer: 400
Show work in this space
a20 = 2n – 1 = 2*20-1=39
Sn = n/2(a1 + an)
Sn = n/2(a1 + a20)
S20 = 20/2(1 + 39)
S20 = 10(40)
S20 = 400
Using the formula for the sum of an arithmetic series, what is the sum of the first 30 terms?
Answer: 900
Show work in this space
a30 = 2n – 1 = 2*30-1=59
Sn = n/2(a1 + an)
Sn = n/2(a1 + a30)
S30 = 30/2(1 + 59)
S30 = 15(60)
S30 = 900
|
|
|
