Question 217318: The third term of an arithmetic sequence is 4 and the sum of the first 8 term is 36. Write down the first 8 term of the sequence.
Answer by drj(1380)   (Show Source): (Show Source):
You can put this solution on YOUR website! The third term of an arithmetic sequence is 4 and the sum of the first 8 term is 36. Write down the first 8 term of the sequence.
Step 1. An arithmetic sequence goes from one term to the next by always adding (or subtracting) the same value
Step 2. Let x be the number to add or subtract in the sequence.
Step 3. Let a be the first term, let a+x be the second term, let a+2x be the third term, a+3x be the fourth term, and a+(n-1)x be the nth term
Step 4. Let a+7x be the 8th term. Then the sum of the first and eighth term is a+a+7x=2a+7x. The sum of the second term and seventh term is the a+x+a+6x=2a+6x. So four the first eight terms, there will be four pairs of 2a+6x which will equal to 36 or

 Equation A Equation A
Also  Equation B since the 3th term is 4. Equation B since the 3th term is 4.
Step 5. Then we have a system of equations given as Equations A and B. The following steps will solve the equation by substitution.
| Solved by pluggable solver: SOLVE linear system by SUBSTITUTION |
Solve:
 We'll use substitution. After moving 7*x to the right, we get: We'll use substitution. After moving 7*x to the right, we get:
 , or , or  . Substitute that . Substitute that
into another equation:
 and simplify: So, we know that x=0.333333333333333. Since and simplify: So, we know that x=0.333333333333333. Since  , a=3.33333333333333. , a=3.33333333333333.
Answer:  . .
|
So a= and x= and x=
So sequence is:  , , 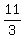 , ,  , , 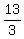 , , 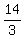 , ,  , , 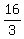 , ,  . .
Check: The third term is  and the sum is and the sum is 
Step 6. ANSWER: The sequence is  , , 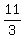 , ,  , , 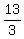 , , 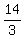 , ,  , , 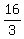 , ,  . .
I hope the above steps and explanation were helpful.
For Step-By-Step videos on Introduction to Algebra,
please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and
for Trigonometry please visit
http://www.FreedomUniversity.TV/courses/Trigonometry.
Also, good luck in your studies and contact me at
john@e-liteworks.com for your future math needs.
Respectfully,
Dr J
|
|
|