Question 212918: The question is: Three consecutive terms of a geometric sequence have a sum of 28 and a product of 512. Find these numbers.
(Hint: let these numbers be a/r, a and ar )
I really don't understand the question, anyone kindly help me??
Thanks
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! A geometric sequence looks like:
7
7*3 = 21
21*3 = 63
63*3 = 189
108*3 = 567
The sequence is:
7,21,63,189,567
In the general formula, I call the nth term 
so,
etc.
The multiplier for each term, in this case,  ,
is called  , and 
All this is saying is:
Another general formula is:
Testing the formula:
If I plug in , then I get
7,21,63,189,567
Now, refering back to your problem, they are just saying
Then, using my formula again
The sequence is:
a, ar, ar^2, ar^3, ar^4
By suggesting that you use a/r, a, and ar, what
they are doing is starting the sequence with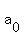 
instead of  , which still gives you a valid sequence
The sequence is
a/r, a, ar, ar^2
Using my example with  ,
the terms would be:
7/3, 7, 21, 63, etc, which is still valid
Three consecutive terms of a geometric sequence have a sum of 28 and a product of 512, so
(1)
(2)
Plugging this into the 1st equation,
(1)
Multiply both sides by
Use the quadratic formua:
|
|
|
