Question 207023: Hi, I was wondering if you can help me with the following problem.
I need to write the following series using the summation notation:
3-6+12-24+48-96
I can tell that you get the next number in the series by multiplying the previous one by -2.... but I don't know where to go from there.
Please help.
Thank You
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, we need to find the sequence that generates the terms. You are correct in that the next term is simply the negative double of the previous term.
So we start with 3 and we multiply by -2 to get -6. Then we multiply -6 by -2 to get 12. What we're really doing is multiplying 3 by -2 twice to get to 12 (since  ). To get -24, we multiply 12 by -2. We could think of it as multiplying by -2 three times like so ). To get -24, we multiply 12 by -2. We could think of it as multiplying by -2 three times like so  . To get 48, we just multiply by 4 negative two's as such . To get 48, we just multiply by 4 negative two's as such  . To shorten these expressions, we can use exponents. So . To shorten these expressions, we can use exponents. So  , ,  , and , and  can replace the last three expressions. can replace the last three expressions.
To get the the nth term (some general unknown term), we need to multiply 3 by 'n'  terms. Or to simplify things, we multiply 3 by terms. Or to simplify things, we multiply 3 by 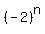 . So the sequence is . So the sequence is  where 'n' starts at n=0. Your book or your teacher may require you to start at n=1. So simply multiply by -2 to shift the entire sequence to get where 'n' starts at n=0. Your book or your teacher may require you to start at n=1. So simply multiply by -2 to shift the entire sequence to get  where 'n' now starts at n=1. where 'n' now starts at n=1.
To keep things simple, I'm going to use the sequence 
So to get the 6th term, we plug in n=6 to get  which is indeed the 6th term (try other values of 'n' to test this sequence) which is indeed the 6th term (try other values of 'n' to test this sequence)
So once we've found the sequence, simply stick it in a summation symbol like so
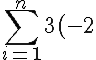^{i-1})
Note: I'm using the variable 'i' (for index) as you'll commonly see this variable used in summations.
Further note: I didn't realize this, but if you want to stop the series at 96, then simply use the summation
^{i-1})
This will simply add up the terms from 3 to 96. In other words,
^{i-1}=3-6+12-24+48-96)
|
|
|