SOLUTION: It is the year 2040 and the Olympics are being held in the People’s Republic of Scotland. The turnout this year is expected to be larger than ever so the Scots have embarked upon

Algebra ->  Algebra  -> Sequences-and-series -> SOLUTION: It is the year 2040 and the Olympics are being held in the People’s Republic of Scotland. The turnout this year is expected to be larger than ever so the Scots have embarked upon      Log On

Ad: Algebrator™ solves your algebra problems and provides step-by-step explanations!
Ad: Algebra Solved!™: algebra software solves algebra homework problems with step-by-step help!

   

Question 172792: It is the year 2040 and the Olympics are being held in the People’s Republic of Scotland. The turnout this year is expected to be larger than ever so the Scots have embarked upon the construction of the largest arena ever created by mankind. This arena will have stadium seating, thus each consecutive row of seating will have more seats than the last. The first row of seats has 300, the second has 350, the third has 400, the fourth has 450 and so on. If there are 700 rows of seating, how many people will the arena sit in total?



Answer by jim_thompson5910(28717) About Me  (Show Source):
You can put this solution on YOUR website!
In this problem (and in future problems), it is VERY critical to know the formula

sum%28i%2Ci=1%2Cn%29=%28n%28n%2B1%29%29%2F2

What this means is the sum from 1 to "n" is equal to %28n%28n%2B1%29%29%2F2. So something like 1%2B2%2B3%2B4%2B5+=+%285%285%2B1%29%29%2F2+=+15



First off, take note that this sequence is an arithmetic sequence (since the difference between each term is the same). So the formula for an arithmetic sequence is

a%5Bn%5D=dn%2Ba%5B1%5D where "d" is the difference between two terms and a%5B1%5D is the first term.

Since the first term is 300, this means that a%5B1%5D=300. Also, because each number is 50 more than the previous one, this means that d=50 (ie the difference is 50)


So the formula for the sequence is a%5Bn%5D=50n%2B300 where "n" starts at 0. To start at n=1, just subtract 50 from 300 to get a%5Bn%5D=50n%2B250 (to shift the terms)


So the formula we'll work with is a%5Bn%5D=50n%2B250 where n%3E=1. So for instance, the third row has 50%283%29%2B250=150%2B250=400 seats (which is what is given)


Now plug in n=700 to find out how many seats are in the 700th row

a%5B700%5D=50%28700%29%2B250=35000%2B250=35250


So there are 35,250 seats in the 700th row

--------------------------------------------


So to find the sum of the seats, we'll add them like this:

300 + 350 + 400 + 450 + ... 35250


Now factor out the GCF 50 to get


50( 6 + 7 + 8 + 9 + ... 705 )


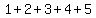Now remember, the formula sum%28i%2Ci=1%2Cn%29=%28n%28n%2B1%29%29%2F2 allows us to sum from 1 to "n". Since we're starting at 6, we need to add in 1%2B2%2B3%2B4%2B5 AND subtract that same amount (to balance things out) like this:


50( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + ... 705 - 1 - 2 - 3 - 4 - 5 )

So it turns out that

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + ... 705 =

and -+1+-+2+-+3+-+4+-+5=-15


So the expression

50( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + ... 705 - 1 - 2 - 3 - 4 - 5 )


becomes


50( 248865 - 15 )


Subtract

50( 248850 )


Multiply


12,442,500


==============================================

Answer:


So there are 12,442,500 seats in the stadium


That's twelve million, four hundred forty two thousand, five hundred seats