please help me solve this sum on summation of series:
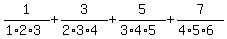 + иии
+ иии
The numerators are the odd numbers, and the nth odd integer
is 2n-1, so that will go on top in the nth term formula. The
denominator of the nth term formula is the product of n and
the next two integers, (n+1) and (n+2), so the nth term is

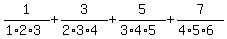 + иии =
+ иии =  Do you understand partial fractions? If not post again
asking how. But I'll assume you already know how.
We break the summand into partial fractions:
Do you understand partial fractions? If not post again
asking how. But I'll assume you already know how.
We break the summand into partial fractions:
 Now suppose we sum this just to some large positive integer K,
and then take the limit as K approaches infinity:
lim
Now suppose we sum this just to some large positive integer K,
and then take the limit as K approaches infinity:
lim  K->oo
Make three sums:
lim
K->oo
Make three sums:
lim  K->oo
Put the constant multipliers in front of the summations:
lim
K->oo
Put the constant multipliers in front of the summations:
lim  K->oo
Make the denominators in the second and third summands all be single
letters, by setting them equal to another letter:
In the second summation, let
K->oo
Make the denominators in the second and third summands all be single
letters, by setting them equal to another letter:
In the second summation, let  or
or  and
in the third summation, let
and
in the third summation, let  or
or  lim
lim  K->oo
lim
K->oo
lim  K->oo
Now no change will result if we replace M and P by n:
lim
K->oo
Now no change will result if we replace M and P by n:
lim  K->oo
In the first summation we write out the first two terms, and
write the summation from n=3 to n=K
K->oo
In the first summation we write out the first two terms, and
write the summation from n=3 to n=K
 In the second summation we write out the first term and the last
term and write the summation from n=3 to n=K
In the second summation we write out the first term and the last
term and write the summation from n=3 to n=K
 In the third summation we write out the last two
terms and write the summation from n=3 to n=K
In the third summation we write out the last two
terms and write the summation from n=3 to n=K
 Now we let
Now we let  So, now the sums become:
So, now the sums become:


 So,
lim
So,
lim  K->oo
becomes:
lim
K->oo
becomes:
lim  K->oo
or:
lim
K->oo
or:
lim  K->oo
Write the
K->oo
Write the 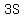 as
as 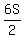 and
and  as
as  lim
lim  K->oo
Ths terms in S all cancel out, and we have
lim
K->oo
Ths terms in S all cancel out, and we have
lim 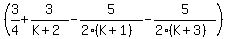 K->oo
The last three terms approach 0 as K approaches infinity.
Therefore the answer is
K->oo
The last three terms approach 0 as K approaches infinity.
Therefore the answer is  Edwin
Edwin