Question 146451: Write the linear function for which f (0) = -4 and f (2) = 8.
Thank you
Found 2 solutions by 24HoursTutor.com, jim_thompson5910:
Answer by 24HoursTutor.com(40)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(0) = -4
f(2) = 8
Which means f(x) = 3x^2 - 4
Let us check for the given functions :
f(0) = 3X0^2 - 4
= 3X0 - 4
= 0 - 4
= -4
f(2) = 3 X 2^2 - 4
= 3 X 4 - 4
= 12 - 4
= 8
Hence, our ans is f(x) = 3x^2 - 4
The above question is solved by one of the experts from 24HoursTutor.com
We provide live 1:1 online homework help
1. 24X7 tutors available
2. Certified tutors
3. Only for $9.99/hr
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm afraid that the previous solution is completely off. The equation "3x^2 - 4" is NOT linear.
f (0) = -4 tells us that when x=0, then y=-4. So the line goes through the point (0,-4)
f (2) = 8 tells us that when x=2, then y=8. So the line goes through the point (2,8)
So let's find the equation of the line that goes through the points (0,-4) and (2,8)
First let's find the slope through the points ) and and )
 Start with the slope formula. Start with the slope formula.
 Plug in Plug in  , ,  , ,  , ,  , , , ,
 Subtract Subtract  from from  to get to get 
 Subtract Subtract  from from  to get to get 
 Reduce Reduce
So the slope of the line that goes through the points ) and and ) is is 
Now let's use the point slope formula:
 Start with the point slope formula Start with the point slope formula
 Plug in Plug in  , ,  , and , and 
 Rewrite Rewrite 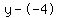 as as 
 Distribute Distribute
 Multiply Multiply
 Subtract 4 from both sides. Subtract 4 from both sides.
 Combine like terms. Combine like terms.
 Simplify Simplify
So the equation that goes through the points ) and and ) is is 
Notice how the graph of  goes through the points goes through the points ) and and ) . So this visually verifies our answer. . So this visually verifies our answer.
 Graph of Graph of  through the points through the points ) and and )
Note: as further confirmation, the graph is a straight line. So this tells us that the equation  is linear. is linear.
|
|
|