Question 1209756: . A construction company purchases a bulldozer for $160.000. Each year the value of the bulldozer depreciates by 20% of its value in the preceding year. Let V, be the value of the bulldozer in the nth year. (Let n = 1 be the year the bulldozer is purchased)
a) Find the formula for V.
12 Marks)
b) In what year will the value of the bulldozer be less than $100.000
(4 Marks)
Found 2 solutions by CPhill, Edwin McCravy:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Here's how to solve this depreciation problem:
**a) Formula for V:**
* **Initial Value:** The bulldozer starts at $160,000.
* **Depreciation Rate:** The bulldozer depreciates by 20% (0.20) each year.
* **Value After 1 Year:** $160,000 * (1 - 0.20) = $160,000 * 0.80 = $128,000
* **Value After 2 Years:** $128,000 * 0.80 = $160,000 * 0.80 * 0.80 = $160,000 * (0.80)²
* **General Formula:** V(n) = $160,000 * (0.80)^(n-1)
**b) Year When Value is Less Than $100,000:**
We want to find the smallest integer *n* such that V(n) < $100,000.
1. **Set up the inequality:**
$160,000 * (0.80)^(n-1) < $100,000
2. **Divide by 160,000:**
(0.80)^(n-1) < 100,000 / 160,000
(0.80)^(n-1) < 0.625
3. **Take the logarithm (base 10 or natural log) of both sides:**
log(0.80)^(n-1) < log(0.625)
(n-1) * log(0.80) < log(0.625)
4. **Divide by log(0.80). Note that log(0.80) is negative, so reverse the inequality sign:**
n - 1 > log(0.625) / log(0.80)
n - 1 > -0.2076 / -0.0969
n - 1 > 2.1424
5. **Add 1 to both sides:**
n > 3.1424
6. **Find the smallest integer:**
Since *n* must be an integer, the smallest value of *n* that satisfies this inequality is *n* = 4.
**Answer:**
a) The formula for V is V(n) = $160,000 * (0.80)^(n-1)
b) The value of the bulldozer will be less than $100,000 in the 4th year.
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website! Looks like AI can solve this type problem. Give AI a few years and it'll be
able to solve any mathematics problem. In the beginning, anybody could beat
AI in chess. But the last time a human could beat AI in chess was in 2008.
It hasn't quite gotten there in mathematics. But give it time and it will!
[In the US, we use a DOT "." for a decimal point, and COMMAS "," to separate
digits in groups of three. It is just the opposite in your country. But nobody
separates digits in groups of three when calculating.]
Since the bulldozer drops in value by 20% each year means that each year, its
value is only 80% of what it was the year before. So, we are talking about the
geometric sequence with first term a1=160,000, and common ratio
r=0.80, and its nth term is an = vn.
(a)
160,000, (0.80)(160000), (0.80)2(160000), (0.80)3(140000),...
  
 
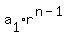
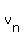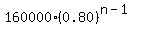(b)
Since it will only take a few years, it's easier to do it this way
The 1st year the value is $160,000.
The 2nd year the value is $160,000(0.80) = $128,000.
The 3rd year the value is $128,000(0.08) = $102,400.
The 4th year the value is $102,000(0.80) = $81,920.
So the 4th year is the first year its value will be less than $100,000 all year.
But your teacher might expect you to use the formula. So you'd do it
this way to please your teacher:
 
 
 
 
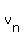
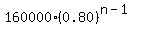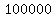
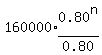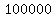
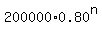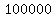
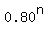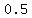
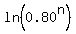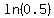
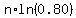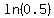
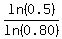
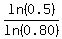
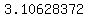So the year after 3.10628372 years its value will be less than $100,000.
That means that the 4th year is the first year its value will be less
than $100,000 all year.
Edwin
|
|
|
