SOLUTION: What is the 1000th value of the following sequence? 1/1,1/2,2/2,1/3,2/3,3/3,1/4,2/4,3/4,4/4,...

1/1,
1/2,2/2,
1/3,2/3,3/3,
1/4,2/4,3/4,4/4,
...

The 1st 1 is term number 1=1 and it is written 1/1
The 2nd 1 is term number 1+2=3 and it is written 2/2
The 3rd 1 is term number 1+2+3=6 and it is written 3/3
The 4th 1 is term number 1+2+3+4=10 and it is written 4/4

The sum of the first k positive integers is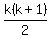 

So

The nth 1 is term number  and it is written n/n

Let's find the term number of the last 1 before the 1000th term





Find the positive zero of the left side by the quadratic formula
and get approximately 44.224

So we substitute 44 in  
 



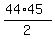
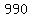So the last 1 before the 1000th term is the 990th term, written as 44/44.

So we either think of, or write out the next 10 terms.

1/45,2/45,3/45,4/45,5/45,6/45,7/45,8/45,9/45,10/45

So the 1000th term is 10/45.

Edwin