SOLUTION: Find two nonnegative numbers whose sum is 9 and so that the product of one number and the square of the other number is a maximum.

Let the second number be x; then the first number is (9-x),

and we want maximize   = .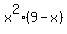


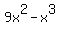Apply Calculus:  take the derivative, equate it to zero, and from this equation find x

    18x - 3x^2 = 0.


We can exclude x= 0, since it is out of our interest, and divide both sides 
of this equation by  3x.  We will get  simpler equation then

    6 - x = 0

    x = 6.


Take the second derivative  18 - 6x  and evaluate the second derivative at x = 6.  
The second derivative value at  x= 6  is  18 - 6*6 = -18.

Since the second derivative is negative at the critical point x= 6, 
we conclude that x= 6 is the desired point of maximum.


The maximum value of the product is  

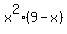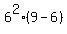     =  = 36*3 = 108.


ANSWER.  The desired numbers are 3 and 6, in this order.