Question 1208339: Find the next term 5, 14, 17, 30,
Found 4 solutions by math_tutor2020, ikleyn, Edwin McCravy, mccravyedwin:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
See this similar question
On that link I try to find the next term in the sequence 1,2,4,...
It turns out there are at least 3 different possible answers for that question. There may be infinitely many answers.
This shows that vague questions like this are very flawed. There needs to be more context provided.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Questions of this form and of this type are mathematically  . .
An arbitrary finite sequence of numbers does not indicate the next term
and does not determine what the next term should be,
until a special separate procedure, a formula or a rule specifies on how to determine the next term.
Therefore, if and when any witch doctor/(woodoo doctor)/(charlatan) gives you a definite answer - know
that you are either being screwed, or deceived, or mocked.
It is known and it is clear to anybody and to everyone, who has
a bit of common sense in his or her brain inside his or her head.
The only correct answer to this question/problem and to million other " problems " of this kind is
"any number can be next term",
but it is, obviously, not what the asking person does expect.
So, please do not post nonsensical problems of this type to this forum in the future.
Thank you very much and have a nice day !
/////////////////////////
Edwin, one standard approach to such problems is to make a row of first differences;
then below it to make next row of second differences
and so on until you get the row consisting of one unique number.
Then it is assumed (without having ani solid base) that all differences of certain order are constant,
and based on it, making backward steps, people restore the original function.
Or, in more simple terms, people simply request and find a polynomial approximation
("exact fit") to the given sequence from online Internet solvers.
Then, using this polynomial, they calculate "the next number" and declare/demonstrate
it as the ANSWER (without having any solid base for it).
The refutation to it is the fact, that we can add another polynomial to the first polynomial
which has zeroes at the given points 1, 2, 3, 4, but has an arbitrary value in the "next point #5".
This is the whole story and the whole tale.
Edwin, you invite me to bring this knowledge to other people.
The world is full of mathematically illiterate people. The number of them is billions.
To me, the TRUTH is clear from the first glance; but I will not spend my time and my efforts
to bring/explain this truth to millions others, where and why they are wrong. For it, they should
have some adequate mathematical education, which they, as a rule, do not have.
How I can convince them, if during the years I can not convince you, who has a university Math education ?
For these people, my advise is to use good sources and do not use bad sources for their Math problems.
Good sources are those that are written by specialists and professionals.
Bad sources are those that are created by all others.
At this forum, the visitors regularly bring their problems "from garbage bins",
but I can do nothing against it (unfortunately).
For such visitors, I only have this standard message, which is the first part
of my post. I keep this message in my archive and use it to respond every time,
as the current nonsensical post/request comes.
Regarding this practice on giving such nonsensical problems as the test for getting jobs,
these people from HR departments deserve to be fired immediately, since they
do not understand what they are doing and are not adequate to their positions.
||||||||||||||||||||||||
In the shortest words, this problem is a puzzle of the most low level -
- of that kind what some charlatans give to unexperienced naive amateurs
to help them to kill their time and to get their money, giving them NOTHING back.
In such puzzles, a correct mathematical solution is impossible, is not required and even is not assumed.
What is required - are these two things:
- (1) amateurs kill their time in exact accordance with their most wanted hidden desire, and they are very happy of it;
- (2) those who create these puzzles for them, leave the scene taking their money in their pockets, and they are happy, too.
Everything else does not matter and does not play any role.
Everybody is satisfied and everybody is happy.
Only me work here in the sweat of the face,
explaining you all details of this backstage.
All such puzzles are 
from the very beginning to the very end.
\\\\\\\\\\\\\\\\\\\\\\\\\\
Edwin, reading your post, I see that you are wonder, why two different logical
reasoning to this puzzle lead to different results.
You should not be surprised. It is completely natural.
It is the same as if two different formulas, applied to 4 given numbers, would lead to different results.
Nobody has ever proved a theorem on the uniqueness of the solution of crazy puzzles.
It is absolutely natural that two different approaches, applied to the given set of input numbers lead to different results.
Simply, let me repeat it again, all this activity around this crazy puzzle is a kind of gibberish.
It is as clear to anybody in healthy mind as 2 x 2 = 4.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
No, Ikleyn, I'm not being a troll. Here are two perfectly correct logical
patterns that give the same four numbers but which produce different
5th numbers. I am doing this to point out something VERY CORRECT that
YOU and another tutor SAID about such problems. Their answers are not unique.
Unfortunately, aptitude tests for getting jobs very often include number
sequences such as this one. I know from personal experience from my younger
years when applying for employment. That's why we should take them seriously.
Maybe to PROTEST AGAINST them! Or else to hopefully get educators to study such
number sequence problems given on such job exams. Somebody should investigate
what is going on with these sequence problems on tests for people interviewing
for jobs. If there are specific types of patterns for them that are required to
answer them, these should be taught in schools.
I made a mistake on the lst one so I deleted it. I had a different one, decided
to change it and forgot to change the numbers in the 5th part. Here is the
corrected version, plus another one below that gives the same results using a
cubic equation in n.
First one (with the numbers corrected in the last step):
Start with 5.
Take the absolute difference between 5 and 9, get 4.
Square 4, get 16, add 26, get 42, divide by 3, get 14.
Take the absolute difference between 14 and 9, get 5.
Square 5, get 25, add 26, get 51, divide by 3, get 17.
Take the absolute difference between 17 and 9, get 8.
Square 8, get 64, add 26, get 90, divide by 3, get 30.
Take the absolute difference between 30 and 9, get 21.
Square 21, get 441, add 26, get 467, divide by 3, get 155 2/3.
Answer 155 2/3.
Second one:
You can also substitute integers 1 through 4 in the following cubic polynomial
in n and get the same 4 numbers you gave.
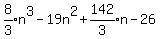 Substituting 1:
Substituting 1:
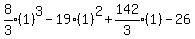

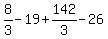
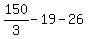
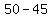
 Substituting 2:
Substituting 2:
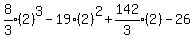
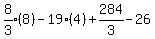
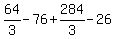
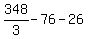
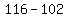
 Substituting 3:
Substituting 3:
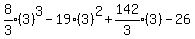
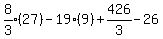
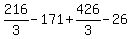
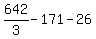
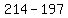
 Substituting 4:
Substituting 4:
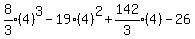

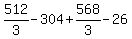
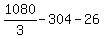
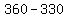
 Substituting 5:
Substituting 5:
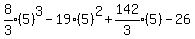
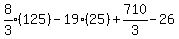

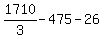
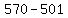
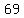 Answer: 69
Edwin
Answer: 69
Edwin
|
|
|