Question 1208200: The 1st term of a g.p is x and the 3rd is y find an expression for the common ratio in terms of x and y
Found 3 solutions by josgarithmetic, mananth, ikleyn:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! The 1st term of a g.p is x and the 3rd is y find an expression for the common ratio in terms of x and y
The general form of a GP = a,ar, ar^2, ar^3
where r is the common ratio
a is the first term
lets replace a with x
x,xr, xr^2, xr^3.......
xr^2=y
r^2=y/x
r = (+-sqrt(y/x))
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If 1st term of a GP is x and 3rd term is y, then
y = 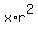 , (1)
where r is the common ratio. If x is not zero, then we can divide both sides of this equation by x , (1)
where r is the common ratio. If x is not zero, then we can divide both sides of this equation by x
 = =  . (2)
Notice that in this case, when x =/= 0, from formula (1), both y and x have the same sign
(both are either positive or negative), so the ratio . (2)
Notice that in this case, when x =/= 0, from formula (1), both y and x have the same sign
(both are either positive or negative), so the ratio  is non-negative.
Hence, we can take square root of is non-negative.
Hence, we can take square root of  r = +/-
r = +/- 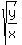 ,
and in the case x =/= 0 it is the final answer to the problem's question,
giving two possible values for r, if y =/= 0, or single zero, of y=0.
In the special case x=0 we CAN NOT divide by x (by zero), so formula (2) does not work.
In this case, the geometric progression is degenerated: all its terms are zeros.
So, the complete answer is r = +/- ,
and in the case x =/= 0 it is the final answer to the problem's question,
giving two possible values for r, if y =/= 0, or single zero, of y=0.
In the special case x=0 we CAN NOT divide by x (by zero), so formula (2) does not work.
In this case, the geometric progression is degenerated: all its terms are zeros.
So, the complete answer is r = +/- 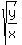 , if x =/= 0 (two possible values, if y =/= 0; or single 0, if y=0)
or any real number, if x = 0, but the GP in this case is degenerated and consists of zeros. , if x =/= 0 (two possible values, if y =/= 0; or single 0, if y=0)
or any real number, if x = 0, but the GP in this case is degenerated and consists of zeros.
Solved completely with giving a complete answer.
--------------------
This problem is, obviously, a trap.
The trap is that a COMPLETE answer is required, including the case x=0.
|
|
|