Question 1205379: Cheyenne tells a joke to 5 people and those 5 people tell the joke to 5 more people, and so on. Which expression shows the number of people that will hear the joke after the sixth round?
Found 3 solutions by MathLover1, math_tutor2020, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! On the first round  people hear the joke people hear the joke
On the second round, those  people each tell people each tell  more people, so more people, so  people hear the joke. people hear the joke.
On the third round, those  people each tell people each tell  more people, so more people, so  people hear the joke. people hear the joke.
On the fourth round, those  people each tell people each tell  more people, so more people, so  people hear the joke. people hear the joke.
On the fifth round, those  people each tell people each tell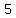 more people, so more people, so people hear the joke. people hear the joke.
On the sixth round, those 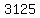 people each tell people each tell  more people, so more people, so  people hear the joke. people hear the joke.
expression  shows the number of people that will hear the joke after the sixth round shows the number of people that will hear the joke after the sixth round
general formula:
 where where  is the number of rounds and is the number of rounds and  the number of people hear the joke the number of people hear the joke
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Open up your favorite spreadsheet program.
I'm using LibreOffice Calc.
In cell A1 will go the label "Round" without quotes.
B1 will have something like "number who heard the joke" without quotes.
C1 will have "Cumulative Sum" without quotes.
Move to cell A2.
Place the number 1 here.
Then grab the bottom right corner of this cell to drag it down until the values 2,3,4,5,6 fill up cells A3 through A7.
Move to cell B2.
Write the number 5 here.
Move to cell B3. Type =5*B2 into cell B3.
The equal sign up front is important. This command marked in blue tells the spreadsheet "multiply whatever is in B2 with the value 5".
The result of cell B3 should be 25.
Grab the bottom right corner of cell B3. Drag it down or doubleclick to populate the remaining values of column B.
The values in column B, from top to bottom, should be: 5, 25, 125, 625, 3125, 15625
Now move to cell C2.
Type =B2 to copy the contents of B2 into C2.
The equal sign is important.
In cell C3 type =B3+C2 to add the contents of those cells. The result is 5+25 = 30
Meaning there are 30 people total who heard the joke at the end of round 2 (the 5 from round 1, and 25 more from round 2, giving 5+25 = 30 total).
Drag the bottom right corner of cell C3 down, or doubleclick to populate the rest of the values.
The values in column C, from top to bottom, should be: 5, 30, 155, 780, 3905, 19530
This is what your spreadsheet should look like
| Round | number who heard joke | Cumulative Sum |
|---|
| 1 | 5 | 5 | | 2 | 25 | 30 | | 3 | 125 | 155 | | 4 | 625 | 780 | | 5 | 3125 | 3905 | | 6 | 15625 | 19530 |
As a check, let's add up the values of everything in column B
5 + 25 + 125 + 625 + 3125 + 15625 = 19530
There are a grand total of 19530 people who have heard the joke after 6 rounds.
Note: This assumes that those who have heard it in any given round do NOT involve people from a previous round.
Eg: if someone heard it in round 3, then they didn't hear it round 1 or round 2.
---------------------------------------------------------
Alternative approach
The sequence 5, 25, 125, 625, 3125, 15625 is geometric.
a = 5 = first term
r = 5 = common ratio
a(n) = a*r^(n-1) = 5*5^(n-1) = number of people who heard the joke on round n
where n is an integer and n = 1 is the starting index.
The expression 5*5^(n-1) is the number of people who heard the joke for that round only, and does not include previous rounds.
To account for previous rounds, we'll need to use the next formula shown below.
Sn = sum of the first n terms of a geometric sequence
Sn = a*(1 - r^n)/(1 - r)
Sn = 5*(1 - 5^n)/(1 - 5)
S6 = 5*(1 - 5^6)/(1 - 5)
S6 = 19530 is the sum of the first 6 terms of this geometric sequence.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
After reading this post, my impression is that it is written and presented with the special goal to confuse a reader.
A meaning of this problem can be understood at least by 4 (four) different ways.
In this form, it is good only to throw it to the closest garbage bin.
|
|
|