Question 1204430: A man borrows 1,000 and agrees to repay with 10 instalments, each instalment being less than the preceding instalment by 8. Find the his first instalment
Found 3 solutions by mananth, math_tutor2020, ikleyn:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here in this problem
amount to be repaid = 1000 Sn =1000
number of instalments =10 n=10
every instalment less by 8 d=-8
Sn=n/2(2a+(n-1)d
Plug and solve for a
1000 =10/5 (2*a+(10-1)*-8
1000/5 = 2*a-72
200= 2a-72
200+72=2a
272/2= a
a=136
The first installment is 136.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a = first installment = first term of arithmetic sequence
n = 10 = number of payments
d = -8 = common difference
Sn = sum of first n terms of arithmetic sequence, aka arithmetic progression (AP)
Sn = 1000
Sn = (n/2)*(2*a + d(n-1))
1000 = (10/2)*(2*a - 8(10-1))
1000 = 5(2a-72)
2a-72 = 1000/5
2a-72 = 200
2a = 200+72
2a = 272
a = 272/2
a = 136
The arithmetic sequence of 10 payments is
136, 128, 120, 112, 104, 96, 88, 80, 72, 64
I used the "sequence" command in GeoGebra to generate this list quickly. A spreadsheet is another good option.
As a check,
136+128+120+112+104+96+88+80+72+64 = 1000
We have confirmed the correct first payment.
An interesting thing to notice is:
(n/2)*(1st term + 10th term) = (10/2)*(136+64) = 1000
Answer: 136
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A man borrows 1,000 and agrees to repay with 10 instalments, each instalment
being less than the preceding instalment by 8. Find the his first instalment
~~~~~~~~~~~~~~~~~~
In this sequence of 10 terms, the in-pair sums of the numbers, equally remoted from the endpoints,
are a constant value:
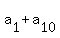 = = 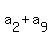 = = 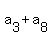 = = 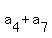 = = 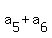 .
Therefore, each in-pair sum is 1000/5 = 200.
So, about the pair .
Therefore, each in-pair sum is 1000/5 = 200.
So, about the pair 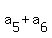 we know that we know that
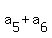 = 200 = 200
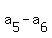 = 8
From it, it is easy to guess/(to derive) that = 8
From it, it is easy to guess/(to derive) that  = 100 + 8/2 = 104.
Now, the term = 100 + 8/2 = 104.
Now, the term  , ,  , ,  , ,  are
104+8 = 112, 112+8 = 120, 120+8 = 128, 128+8 = 136, respectively.
Thus, the first term (= the first installment) is 136. ANSWER are
104+8 = 112, 112+8 = 120, 120+8 = 128, 128+8 = 136, respectively.
Thus, the first term (= the first installment) is 136. ANSWER
Solved / mentally.
|
|
|