|
Question 1204296: Find the sum of the digit of a 3 digit integers
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946)   (Show Source): (Show Source):
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the sum of the  digits of digits of  3 digit integers 3 digit integers
~~~~~~~~~~~~~~~~~~~~~
Attention to the visitor (and to the problem's creator)
If you want to avoid misreading and misunderstanding, write "three-digit integers"
instead of "3 digit integers", as this standard form is traditionally accepted in Math.
Solution
Three-digit integers are from 100 to 999. In all, there are 999 - 99 = 900 such integer numbers.
The ones digits are from 0 to 9.
Each ones digit from 0 to 9 is repeated with the same frequency;
the number of different digits is 10 and the frequency of each digit is 900/10 = 90.
So, the sum of all digits in the ones position is 90 times (1 + 2 + 3 + . . . + 9) = 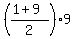 = 5*9 = 45.
90 times 45 is 90*45 = 4050. Thus the sum of all 900 ones digits is 4050.
The tens digits are from 0 to 9.
Each tens digit from 0 to 9 is repeated with the same frequency;
the number of different digits is 10 and the frequency of each digit is 900/10 = 90.
So, the sum of all digits in the tens position is 90 times (1 + 2 + 3 + . . . + 9) = = 5*9 = 45.
90 times 45 is 90*45 = 4050. Thus the sum of all 900 ones digits is 4050.
The tens digits are from 0 to 9.
Each tens digit from 0 to 9 is repeated with the same frequency;
the number of different digits is 10 and the frequency of each digit is 900/10 = 90.
So, the sum of all digits in the tens position is 90 times (1 + 2 + 3 + . . . + 9) = 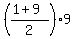 = 5*9 = 45.
90 times 45 is 90*45 = 4050. Thus the sum of all 900 tens digits is 4050.
The hundreds digits are from 1 to 9.
Each hundreds digit from 1 to 9 is repeated with the same frequency;
the number of different digits is 9 (the zero is not included) and the frequency of each digit is 900/9 = 100.
So, the sum of all digits in the hundreds position is 100 times (1 + 2 + 3 + . . . + 9) = = 5*9 = 45.
90 times 45 is 90*45 = 4050. Thus the sum of all 900 tens digits is 4050.
The hundreds digits are from 1 to 9.
Each hundreds digit from 1 to 9 is repeated with the same frequency;
the number of different digits is 9 (the zero is not included) and the frequency of each digit is 900/9 = 100.
So, the sum of all digits in the hundreds position is 100 times (1 + 2 + 3 + . . . + 9) = 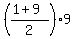 = 5*9 = 45.
100 times 45 is 100*45 = 4500. Thus the sum of all 900 hundreds digits is 4500.
Now the ANSWER to the problem's question is this sum 4050 + 4050 + 4500 = 12600. = 5*9 = 45.
100 times 45 is 100*45 = 4500. Thus the sum of all 900 hundreds digits is 4500.
Now the ANSWER to the problem's question is this sum 4050 + 4050 + 4500 = 12600.
Solved.
------------------
In this problem, there is an underwater stone, so be CAREFUL:
- the frequency of digits in the hundreds position (100)
is not the same as that in the tens and/or in the ones position (90).
///////////////////
As I see from the post, the level of the problem's creator in Math is quite low, same as in English.
|
|
|
| |