Question 1203795: the second term of an arithmetic is 12 and the 6th term is 40. What is the common difference?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a1 = first term, a2 = second term, etc
d = common difference = the gap from term to term
a2 = 12
a3 = a2 + d = 12 + d
a4 = a3 + d = (12+d) + d = 12+2d
a5 = a4 + d = (12+2d) + d = 12+3d
a6 = a5 + d = (12+3d) + d = 12+4d
a6 = 40
12+4d = 40
4d = 40-12
4d = 28
d = 28/4
d = 7 is the common difference
Verification
a2 = 12
a3 = a2 + d = 12+7 = 19
a4 = a3 + d = 19+7 = 26
a5 = a4 + d = 26+7 = 33
a6 = a5 + d = 33+7 = 40
We arrive at a6 = 40 to confirm the answer is correct.
The sequence is 5,12,19,26,33,40,... that starts at 5 and increments by 7 each time we need a new term.
Answer by ikleyn(52802)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Between the 2nd and the 6th terms of an AP, there are 6-2 = 4 gaps of equal length on the number line.
Each gap is 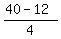 = = 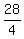 = 7 units long.
The size of each gap is exactly the common difference value.
So, the common difference of this AP is 7 units. = 7 units long.
The size of each gap is exactly the common difference value.
So, the common difference of this AP is 7 units.
Simple, short and elegant reasoning.
It makes sense to memorize this mantra an use it
in many other similar problems to provide quick solutions.
|
|
|