SOLUTION: Calculate the sum between and including the terms t16 and t53 of an arithmetic sequence with first term 543 and common difference - 12.

Algebra ->  Sequences-and-series -> SOLUTION: Calculate the sum between and including the terms t16 and t53 of an arithmetic sequence with first term 543 and common difference - 12.      Log On


   

Question 1202468: Calculate the sum between and including the terms t16 and t53 of an arithmetic sequence with first term 543 and common difference - 12.
Found 4 solutions by mananth, greenestamps, ikleyn, MathTherapy:
Answer by mananth(16946) About Me  (Show Source):
You can put this solution on YOUR website!
Calculate the sum between and including the terms t16 and t53 of an arithmetic sequence with first term 543 and common difference - 12.
a= 543
d= 12
Sn = n/2(2a+(n-1)d
Sum of 16 terms
S16 = 16/2(2*(543)+15*12) =10128
Sum of 53 terms
S53 = 53/2(2*543+52*12) =45315
Find the difference between them
t16 = a+15d
t16= 543+15*12=723
t53 = a+52d
=543+52*12 =1167
Sum including these terms t16 and t53
Think it over

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The response from the other tutor has at least a couple of significant errors, starting with a common difference of 12 instead of -12.

Overlooking those errors, her presentation of the solution does little to help the student learn.

The sequence consisting of the 16th through 53rd terms of an arithmetic sequence is itself an arithmetic sequence.

The first term of that sequence (the 16th term of the original sequence) is the first term of the original sequence, plus the common difference 15 times: 543%2B15%28-12%29=543-180=363.

The last term of the new sequence ( the 53rd term of the original sequence) is the first term of the original sequence, plus the common difference 52 times: 543%2B52%28-12%29=543-624=-81.

The number of terms in the new sequence is %2853-16%29%2B1=38.

The sum of the terms of the new sequence is the number of terms, times the average of the first and last terms: 38%28%28363-81%29%2F2%29=38%2A141=5358.

ANSWER: 5358

Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
Calculate the sum between and including the terms t16 and t53 of an arithmetic sequence
with first term 543 and common difference -12.
~~~~~~~~~~~~~~~~~~~~


            The solution by @mananth is a pile of mistakes,
            that do not deserve to analyse them.

            I came to bring a correct solution. 


There are two ways to solve the problem.


                          First way


The needed sum is the difference  S(t16,t53) = S(53) - S(15).      (1)



The sum of the first 53 terms is (use the standard formula for the sum
of n first terms of an AP)

    S(53) = 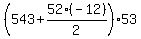%28a%5B1%5D+%2B+%28%28n-1%29%2Ad%29%2F2%29%2An = %28543+%2B+52%2A%28-12%29%2F2%29%2A53 = 12243.     (2)



The sum of the first 15 terms is (use the same standard formula for the sum
of n first terms of an AP)

    S(15) = %28a%5B1%5D+%2B+%28%28n-1%29%2Ad%29%2F2%29%2An = %28543+%2B+14%2A%28-12%29%2F2%29%2A15 = 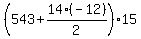6885.      (3)


Now the  ANSWER  is the difference of numbers (2) and (3), according to (1):

    S(t16,t53) = S(53) - S(15) = 12243 - 6885 = 5358.             (4)    ANSWER



                          Second way


Second way is to calculate the terms of this AP

    t16 = 543 + (16-1)*(-12) = 363,  t53 = 543 + (53-1)*(-12) = -81,


and then use another standard formula for the sum 

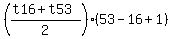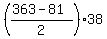    S(t16,t53) = %28%28t16%2Bt53%29%2F2%29%2A%2853-16%2B1%29 = %28%28363+-+81%29%2F2%29%2A38 = 5358.    (5)


We get the same number/answer as in (4).


ANSWER.  The needed sum is 5358,  calculated in two different ways.

Solved.


//////////////////


Regarding work of @mananth at this forum, I always repeat it many times,
that his work can be successful under two indispensable conditions:

        - two persons should assist him: one to explain him what to do,
          and the second to re-write and edit his compositions after him.



Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Calculate the sum between and including the terms t16 and t53 of an arithmetic sequence with first term 543 and common difference  -  12.

use the A.P. formula to get the value of term 16 (t16 or a16).
So, we get: matrix%281%2C3%2C+a%5Bn%5D%2C+%22=%22%2C+a%5B1%5D+%2B+%28n+-+1%29d%29 ---- Formula for a specific term of an A.P./A.S.
           

Now, we use the formula for the sum of an A.P. series from term 16 to term 53. The number of terms (n) in this series = 38 (53 - 16 + 1)
Additionally, note that since we're summing the values from the 16th term to the 53rd term, we will use term 16 as the 1st term of the series.

So, we get: matrix%281%2C3%2C+S%5Bn%5D%2C+%22=%22%2C+%28n%2F2%29%282a%5B1%5D+%2B+%28n+-+1%29d%29%29 ---- Formula for the sum of an A.P./A.S.
            ---- Substituting 38 for n, 363 for a1, and - 12 for d
           

From term 16 (t16, or a16) to term 53 (t53, or a53), SUM of the series, or S38 = 19(282) = 5,358

OR

Find the sum of ALL 53 terms:
            matrix%281%2C3%2C+S%5Bn%5D%2C+%22=%22%2C+%28n%2F2%29%282a%5B1%5D+%2B+%28n+-+1%29d%29%29 ---- Formula for the sum of an A.P./A.S.
            ---- Substituting 53 for n, 543 for a1, and - 12 for d
           

SUM of ALL 53 terms = 53(231) = 12,243

Find the sum of the FIRST 15 terms:
            matrix%281%2C3%2C+S%5Bn%5D%2C+%22=%22%2C+%28n%2F2%29%282a%5B1%5D+%2B+%28n+-+1%29d%29%29 ---- Formula for the sum of an A.P./A.S.
            ---- Substituting 15 for n, 543 for a1, and - 12 for d
           

SUM of FIRST 15 terms = 15(459) = 6,885

Now, SUBTRACT the SUM of the 1st 15 terms from the SUM of ALL 53 terms to get the SUM of terms 16 to 53.
This is: 12,243 - 6,885 = 5,358