.
Calculate the sum of the series: - 396 - 308 - 220 - 132 - ... + 836.
~~~~~~~~~~~~~~~~~~~
The sequense -396, -308, -220, -132, . . ., 836 is an arithmetic progression
with the first term a= -396 and the common difference of d= 88
(sinse -308 - (-396) = 88 and each next term is 88 units greater than the current term).
Find the number of term. Use the formula for the n-th term
836 = -396 + 88*(n-1).
It gives (836 + 396) = 88*(n-1); n-1 = 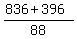 = 14; hence, n= 15.
CHECK. -396 + (15-1)*88 = use your calculator = 836, correct.
To find the sum of this AP, use the general formula for the sum of an AP
= 14; hence, n= 15.
CHECK. -396 + (15-1)*88 = use your calculator = 836, correct.
To find the sum of this AP, use the general formula for the sum of an AP
 =
=  .
It gives at n= 15
.
It gives at n= 15
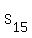 =
= 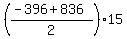 = use your calculator = 3300. ANSWER
= use your calculator = 3300. ANSWER
Solved.
----------------
For introductory lessons on arithmetic progressions see
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
in this site.
/////////////////
Now you see from my post (I hope), how much is it better
to post problems separately than to pack them in sets.
It is the ONLY way to communicate with tutors in a respectful tone.
Do not forget to post your " THANKS " to me for my teaching.