Question 1201935: For positive numbers a, b, and c, if 2ab = 1, 3bc = 2, and 4ca = 3, what is the value of a + b + c ?
(A) 29/12
(B) 9/4
(C) 25/12
(D) 23/12
(E) 7/4
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: Choice (A) 29/12
Explanation:
I'll label the equations eq1, eq2, and eq3
Divide eq1 over eq2.
The LHS (left hand sides) and RHS (right hand sides) will divide separately.
eq1/eq2
(2ab)/(3bc) = 1/2
(2a)/(3c) = 1/2
a/c = (1/2)*(3/2)
a/c = 3/4
4a = 3c
Now multiply both sides by 'c' so the 4a becomes 4ca.
c*4a = c*3c
4ca = 3c^2
3 = 3c^2 ... replace 4ca with 3; valid because of eq3
3c^2 = 3
c^2 = 3/3
c^2 = 1
c = sqrt(1) ... since c is positive
c = 1
Go back to eq3 to determine 'a'.
4ca = 3
4*1a = 3
4a = 3
a = 3/4
Now use either eq1 or eq2 to find b
2ab = 1
2*(3/4)*b = 1
(6/4)*b = 1
(3/2)*b = 1
b = 1*(2/3)
b = 2/3
or
3bc = 2
3b*1 = 2
3b = 2
b = 2/3
We found these values
a = 3/4
b = 2/3
c = 1
Add them up.
a + b + c
(3/4) + (2/3) + 1
(3/4)*(3/3) + (2/3)*(4/4) + 1*(12/12)
(9/12) + (8/12) + (12/12)
(9+8+12)/12
29/12
Extra info:
The improper fraction 29/12 converts to the mixed number 2 & 5/12 because of the scratch work below.
29/12 = (24+5)/12
29/12 = (24/12)+(5/12)
29/12 = 2+(5/12)
29/12 = 2 & 5/12
Or you could use long division to find that 29/12 = 2 remainder 5. Both of these values are found in "2 & 5/12".
The template is quotient & remainder/12.
29/12 = 2.41667 approximately
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For positive numbers a, b, and c, if 2ab = 1, 3bc = 2, and 4ca = 3, what is the value of a + b + c ?
(A) 29/12
(B) 9/4
(C) 25/12
(D) 23/12
(E) 7/4
~~~~~~~~~~~~~~~~
The solution by @math_tutor is correct, but can make you shudder.
I will show you an elegant, simple and fine STANDARD solution to this
and similar problems, which will make you more than happy.
From the given info, we have these equations
ab =  (1)
bc = (1)
bc =  (2)
ac = (2)
ac =  (3)
Multiply all these three equations (their left sides and their right sides separately). You will get
a^2*b^2*c^2 = (3)
Multiply all these three equations (their left sides and their right sides separately). You will get
a^2*b^2*c^2 = 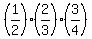 = =  ,
or
(a*b*c)^2 = ,
or
(a*b*c)^2 =  .
Take the square root of both sides. Since "a", "b", and "c" are positive, it gives you
a*b*c = .
Take the square root of both sides. Since "a", "b", and "c" are positive, it gives you
a*b*c =  . (4)
At this point, you may find "a", "b" and "c" separately.
To find "a", divide (4) by (2);
To find "b", divide (4) by (3);
To find "c", divide (4) by (1).
You will get a = . (4)
At this point, you may find "a", "b" and "c" separately.
To find "a", divide (4) by (2);
To find "b", divide (4) by (3);
To find "c", divide (4) by (1).
You will get a = 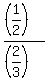 = =  ; b = ; b =  = =  ; c = ; c = 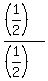 = 1.
Now a + b + c = = 1.
Now a + b + c =  + +  + 1 = + 1 =  + + 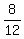 + +  = =  + +  = = 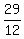 . ANSWER . ANSWER
Solved.
---------------
Memorize this method and use it for other similar problems.
|
|
|