Question 1200343: For which values of n is the terms value equal to the sum of the terms to that point in the
The arithmetic sequence ; 7,5,3
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For which values of n is the terms value equal to the sum of the terms to that point in the
the arithmetic sequence 7,5,3, . . .
~~~~~~~~~~~~~~~~
You are given first three terms of an arithmetic progression 7, 5, 3.
As you see, each next term is 2 units less than the previous term.
Using this rule, continue the sequence further
7, 5, 3, 1, -1, -3, -5, -7, -9.
Now take the sum of written terms.
Do not worry: it is easy to calculate the sum, because in the sum
the negative terms will kill the positive terms.
The only term, which will survive is the term -9.
So, the sum of this sequence is -9.
At the same time, the value of -9 is the 9-th term of the progression.
Doing this way, you just answered the problem's question:
+---------------------- A N S W E R --------------------------+
| the value of "n" (the number of terms) when |
| the sum of progression is equal to its n-th term, is 9. |
+-------------------------------------------------------------+
Solved, answered and explained.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The problem says the n-th term is the sum of the first n terms of the sequence. Since we count with positive numbers, n has to be positive.
The numbers in the sequence are decreasing, so as we keep adding terms of this sequence, the sum will quickly become negative.
Note also that, since the terms are all odd and the sequence is decreasing, in evaluating the sum of the terms to a particular point the later terms will cancel the earlier terms.
It should be clear that when the term -7 is added, the sum of the terms of the sequence will be 0; so the last time the sum of the terms is positive is when the term -5 is added. That sum is
7 + 5 + 3 + 1 + (-1) + (-3) + (-5) = 7
And that sum is the sum of the first 7 terms of the sequence, so the conditions of the problem are satisfied. The sum of the first 7 terms of the sequence is 7, so
ANSWER: 7
For practice with the formal algebra for working with sums of arithmetic sequences, solving the problem using formal mathematics is a useful exercise.
The sum of n terms of an arithmetic sequence is the number of terms, n, multiplied by the average of the terms. And in an arithmetic sequence, the average of all the terms is the average of the first and last.
Given first term a and common difference d, the n-th term of the sequence is a+(n-1)d.
In this problem, a=7 and d=-2; so the n-th term is 7+(n-1)(-2) = 7-2n+2 = 9-2n.
The sum of the first n terms (number of terms, times the average of the terms) is then
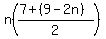
And we want that sum to be the number of the term:





|
|
|