Question 1199359: In a geometric sequence of real numbers, the sum of the first
two terms is 7 and the sum of the first six terms is 91. What is the sum of
the first four terms?
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a geometric sequence of real numbers, the sum of the first
two terms is 7 and the sum of the first six terms is 91. What is the sum of
the first four terms?
~~~~~~~~~~~~~~
We are given
 + +  = 7 (1) = 7 (1)
 + +  + +  + +  + +  + +  = 91 (2)
In terms of "a" (the first term) and "r" (the common ratio) these equalities take the form
a + ar = 7, (3)
a + ar + = 91 (2)
In terms of "a" (the first term) and "r" (the common ratio) these equalities take the form
a + ar = 7, (3)
a + ar + 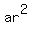 + + 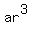 + + 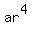 + + 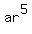 = 91 (4)
In (4), group the terms
(a + ar) + ( = 91 (4)
In (4), group the terms
(a + ar) + (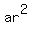 + + 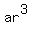 ) + ( ) + (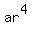 + + 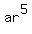 ) = 91. (5)
Re-write (5) in an equivalent form
(a + ar) + ) = 91. (5)
Re-write (5) in an equivalent form
(a + ar) + 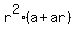 + + 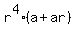 ) = 91. (6)
In (6), replace (a+ar) by the value of 7, based on (3). You will get
7 + ) = 91. (6)
In (6), replace (a+ar) by the value of 7, based on (3). You will get
7 + 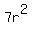 + + 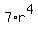 = 91. (7)
In (7), divide both sides by 7
1 + = 91. (7)
In (7), divide both sides by 7
1 +  + + 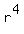 = 13,
or = 13,
or
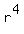 + +  - 12 = 0. (8)
This biquadratic equation (8) is the quadratic equation relative - 12 = 0. (8)
This biquadratic equation (8) is the quadratic equation relative  . Solve it by factoring . Solve it by factoring
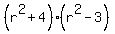 = 0
Since we are given that the progression is in real numbers, = 0
Since we are given that the progression is in real numbers, 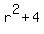 can not be zero
(it is positive at any real r), we conclude that only possible value of can not be zero
(it is positive at any real r), we conclude that only possible value of  is is
 = 3.
Then for the sum of the first four terms of this geometric progression = 3.
Then for the sum of the first four terms of this geometric progression 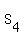 we have we have
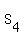 = a + ar + = a + ar + 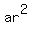 + + 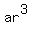 = (a + ar) + ( = (a + ar) + (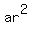 + + 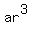 ) = (a+ar) + ) = (a+ar) + 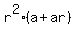 .
We substitute here a+ar = 7 and .
We substitute here a+ar = 7 and  = 3, and we get = 3, and we get
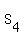 = 7 + 3*7 = 7 + 21 = 28.
ANSWER. The sum of the first 4 terms of this GP is 28. = 7 + 3*7 = 7 + 21 = 28.
ANSWER. The sum of the first 4 terms of this GP is 28.
Solved.
|
|
|