Question 1197650: 2nd question:
the terms a,m,n,b form an arithmetic sequence.Express m and n in terms of a and b.(The terms m and n are arithmetic means of the terms a and b.)
Method I 've tried: d=(b-a)/3
Thank you.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
You are on the right track to arrive at d = (b-a)/3
Nice work so far.
=======================================================
Given: a,m,n,b form an arithmetic sequence
What this means is:
a = first term
m = second term = a+d
n = third term = m+d = (a+d)+d = a+2d
b = fourth term = n+d = (a+2d)+d = a+3d
Where d is the common difference. It's the length of the gap between terms.
For a more numeric and concrete example, the arithmetic sequence 1,3,5,7,9 has a common difference of d = 2 as this is the gap between terms (eg: 7-5 = 2)
Each time we need a new term to the sequence, add on d.
Let's focus on the line that says
b = fourth term = n+d = (a+2d)+d = a+3d
or in short
b = a+3d
Let's solve for d.
b = a+3d
b-a = 3d
d = (b-a)/3
This matches with what you got. You are correct so far.
Whatever the values of 'a' and b are, we find their difference and split it into 3rds to determine d.
This is to be expected. Imagine a yard stick where we split into 3 equal pieces. The two cut points will be exactly m and n, which represent 1/3 and 2/3 along the entire stick.
'a' and b represent the left most and right most parts of the stick before any cuts were made.
If you're a bit lost, then the visual section below might help clear things up.
We'll use this value of d to determine m and n in terms of 'a' and b only
m = a+d
m = a+(b-a)/3
m = 3a/3 + (b-a)/3
m = (3a+(b-a))/3
m = (2a+b)/3
and
n = a+2d
n = a+2(b-a)/3
n = 3a/3 + (2b-2a)/3
n = (3a+2b-2a)/3
n = (a+2b)/3
It's a bit interesting how we have the swap of coefficients when going from 2a+b to a+2b.
=======================================================
Here's a visual to see why this works out
In the diagram above, (b-a) represents the length on the number line from 'a' to b
d = (b-a)/3 is the result of splitting this interval into 3 equal pieces.
The cuts are at m and n
In the diagram, I made the distance form 'a' to b exactly 9 units (take note of the grid lines on the graph paper). But you can change this total distance to whatever you like and the same concepts will still apply.
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
As you started your solution, it was absolutely right way.
I only do not understand why you stopped there, where you stopped and did not go to the end.
The reasoning is very simple and intuitively is obvious.
We should place two terms "m" and "n" between given numbers "a" and "b" in a way that
four terms a, m, n, b form an AP.
So, between the extreme terms "a" and "b", there are three gaps of equal length.
Hence, each gap is 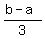 , and therefore
m =  + =  =  ,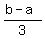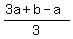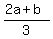
n =  - =  =  .
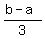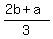That's all. At this point, the solution is complete.
Solved.
|
|
|
