Question 1195898: https://artofproblemsolving.com/texer/japjtbbh
Suppose that 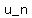 is a sequence of real numbers satisfying is a sequence of real numbers satisfying  , and that , and that  and and  . What is . What is 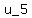 ? ?
*Edited
Found 3 solutions by ikleyn, math_tutor2020, lotusjayden:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose that u_n is a sequence of real numbers satisfying u_(n+1) = 2u_(n+1) + u_n,
and that u_3=9 and u_6=128. What is u_5 ?
~~~~~~~~~~~~~~
From the basic formula
u_(n+1) = 2u_(n+1) + u_n
you have, reducing the term u_(n+1) in both sides,
0 = u_(n+1) + u_n,
or, EQUIVALENTLY,
u_(n+1) = -u_n.
This formula means that the terms {u_n}, as a sequence, simply change the sign, from any given term to the next one.
Having it in mind, you may conclude that the problem is posed INCORRECTLY,
since u_6 must be -9 then.
This notice completes the solution.
ANSWER. The problem is posed INCORRECTLY: it is SELF-CONTRADICTORY.
-----------------
comment from student: Ooops! I revised it here:https://artofproblemsolving.com/texer/japjtbbh
My response : In such cases, you should apology and re-submit your problem to the forum, again.
I will solve the updated version below.
///////// - - - the updated version - - - \\\\\\\\\\\
Suppose that u_n is a sequence of real numbers satisfying u_(n+2) = 2u_(n+1)+u_n,
and that u_3=9 and u_6=128. What is u_5?
~~~~~~~~~~~~~~~~~~~
Let x be u_4.
My goal is to find x from given data.
Then I will be in position to find u_5.
So, for u_5 I have then, using the basic formula
u_5 = 2u_4 + u_3 = 2x + 9.
For u_6 I will have
u_6 = 2*u_5 + u_4 = 2*(2x+9) + x = (4x+18) + x = 5x + 18.
From the other side hand, u_6 = 128 (given).
It gives me an equation
5x + 18 = 128
or
5x = 128-18 = 110,
x 110/5 = 22.
Now u_5 = 2u_4 + u_3 = 2x + 9 = 2*22 + 9 = 44 + 9 = 53.
ANSWER. u_5 = 53.
Solved.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If the sequence is
u_(n+1) = 2u_(n+1) + u_(n)
then you will arrive at the conclusion that @ikleyn reached: in that the terms should alternate in sign.
However, assuming that u3 = 9 and u6 = 128 are correct, then there's no way the above sequence works.
--------------------------------------------------------------------------
I noticed that your link mentioned this instead
u_(n+2) = 2u_(n+1) + u_(n)
The n+1 portion at the front was changed to n+2
If that's the case, then we can say the following two equations
u6 = 2*u5 + u4
u5 = 2*u4 + u3
Let,
x = u5
y = u4
and furthermore we are given,
u3 = 9
u6 = 128
So those two equations mentioned update to
128 = 2*x + y
x = 2*y + 9
after plugging in the given knowns and unknowns.
Apply substitution to solve for y.
128 = 2*x + y
128 = 2*(2y+9) + y
128 = 4y+18 + y
128 = 5y+18
5y+18 = 128
5y = 128-18
5y = 110
y = 110/5
y = 22
Let's find x based on that.
x = 2y+9
x = 2*22+9
x = 44+9
x = 53
Since x = 53 and y = 22, we can then say: u5 = 53 and u4 = 22
Check:
u3 = 9
u4 = 22
u5 = 2*u4+u3 = 2*22+9 = 44+9 = 53
u6 = 2*u5+u4 = 2*53+22 = 106+22 = 128
The answer is fully confirmed.
Again this all hinges on the assumption that the sequence is u_(n+2) = 2u_(n+1) + u_(n)
Answer by lotusjayden(18)   (Show Source): (Show Source):
|
|
|