Question 1194395: I starting to learn about mathematical induction, and I'm not sure if my answers are correct. Please help.
Here is the question, my answers are inside brackets, the rest is provided by the exercise. Thank you.
Complete the following proof by mathematical induction that, for all n in W such that n >= 2, 3 ^ n > 2 ^ (n + 1)
We proceed by mathematical induction and begin by establishing the base of the induction.
3^ 2 = [9] > [8] =2^ 2+1
We see that 3 ^ n > 2 ^ (n + 1) when n=2.
Moving on to the induction step, we suppose that m in W is such that m >= 2
and as our induction hypothesis, we take the assumption that 3^m > 2 ^ (m + 1)
Noting that 3m+is the product of one more 3 than 3 ^m+1 and that 2 ^ (m + 2) is the product of one more 2 than 2 ^ (m + 1)
We calculate as follows:
2 ^ (m + 1) + 1 = [ 2 * 2 ^ (m + 1) ]
(choose from; 2+2^(m+1), 2.2^(m+1), 2^(m+1) +1)
= [ 2^ m+1 +2^ m+1 ]
(choose from; 2^m*2^m, 2^m+2^m, 2^(m+1)+2^(m+1))
< 3^m +2^m+1 by the induction hypothesis and additive monotonicity
< [ 3^m + 2 ^ m + 2^m ] by the induction hypothesis and additive monotonicity
(choose from; 3^m + 2^m + 2^m, 3^m +3^m, 3^m + 3^(m+1) )
< [ 3^m + 3^m + 3^m ] by order in W since 3^ m is in N
(choose from; 3^m *3^m, 3m +3^(m+1), 3^m + 3^m + 3^m )
= [3*3^m ]
(choose from, 3*3^m, 3^m*3^m, 3+3^m )
=3^ m+1
We have shown that 3 ^ 2 > 2 ^ (2 + 1) and that, for all m in W such that m >= 2, if * 3 ^ m > 2 ^ (m + 1)
then 3 ^ (m + 1) > 2 ^ (m + 1) + 1
We may therefore conclude by mathematical induction that, for all n in W such that n >= 2; 3 ^ n > 2 ^ (n + 1)
Found 2 solutions by math_helper, ikleyn:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I think your base case and hypothesis are fine. You could have made the step case (m+1) clearer, as follows:
base: n=2,  > >  base case n=2 holds base case n=2 holds
hypothesis: Assume 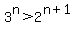 for some m, where m>2. for some m, where m>2.
step case: Let n=m+1:
Need to show 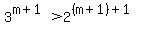
LHS: 
RHS: 
We now apply the hypothesis 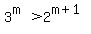
and can conclude LHS > RHS, i.e. 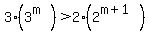
(for A > 0 and B > 0, if A > B than certainly 3A > 2B).
or, re-writing, 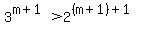
Done
Usually, in inductive proofs, you should be looking to reduce the 'n+1' case to something involving 'n' so that you can directly apply the hypothesis, then include that new information into the 'n+1' scenario and draw the final conclusion.
Answer by ikleyn(52788)   (Show Source): (Show Source):
|
|
|