Question 1193591: Find the sum of this series that is not arithmetic or geometric,
1+2+4+5+7+8....+95+97+98
can someone help, a few of us have been trying to figure this out, our teacher said its solvable but I don't even know where to start, thankyou
Found 3 solutions by math_tutor2020, ikleyn, greenestamps:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Hint:
Notice the odd-numbered terms (first, third, fifth, etc) follow this sequence 1, 4, 7, ...
While the even-numbered terms (second, fourth, sixth, etc) follow this sequence 2, 5, 8, ...
Both subsequences are arithmetic and have a common difference of d = 3 but different starting values of 
Find the nth term formula for each using  as your template.
The nth term formulas will help determine where the 95, 97 and 98 end up; thereby determining how many terms are in each subsequence (i.e. the value of n).
Afterward, use the formula
to find the sum of the first n terms for each arithmetic subsequence.
The final task is to add the two resulting sums to get your final answer.
If you have further questions, then please let me know. Or feel free to post again on the algebra.com website
Answer by ikleyn(52788)  (Show Source):
You can put this solution on YOUR website! .
Find the sum of this series that is not arithmetic or geometric,
1+2+4+5+7+8....+95+97+98
can someone help, a few of us have been trying to figure this out,
our teacher said its solvable but I don't even know where to start, thankyou
~~~~~~~~~~~~~~~~~~
The major problem with your post is that it is BAD STYLE presenting a Math task.
Actually, in your post the problem is not posed as a Math problem.
The reader should guess what this sequence/series is.
When a reader should guess what the author wants to say, it is just not a Math problem.
So, I will re-formulate it to present it in a way, as it SHOULD be presented.
+------------------------------------------------------------------------+
| In the sequence of 99 first natural numbers from 1 to 99 inclusive, |
| each third term is removed. Find the sum of remaining numbers. |
+------------------------------------------------------------------------+
Now it is normal Math entertainment problem.
For the solution, the reader should know that the sum of the first n natural numbers is  .
It is one of the basic facts about arithmetic progressions.
If you don't know it, you may derive this formula, but then the problem itself is not an entertainment - it is just
full size study piece of knowledge.
So, to keep this style of entertainment problem, I will assume that you know this formula.
If so, then the entire problem is two easy steps.
First, the sum of natural numbers from 1 to 99 is 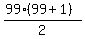 =  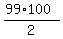= 99*50 = 4950.
From it, we should subtract the sum of all "removed" terms, which is
3 + 6 + 9 + . . . + 96 + 99 = 3*(1 + 2 + 3 + . . . + 32 + 33).
In the parentheses, we have the sum of the first 33 natural numbers, which is  = 33*17 = 561.
Now your ANSWER is this difference 4950 - 3*561 = 3267.
Solved (keeping the style of an entertainment problem).
-------------------
For introductory lessons on arithmetic progressions see
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Also, did your mother or other relatives teach you to thank those who help you ?
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
You have received two responses that show two very different ways of solving the problem, both of which are valid.
Here is a third (still very different) method....
The sequence is clearly neither geometric nor arithmetic. But we can make it into an arithmetic sequence by pairing the terms:
1+2=3
4+5=9
7+8=15
.
.
.
97+98=195
So the sum is
3+9+15+...+195
That is an arithmetic sequence with first term 3, last term 195, and common difference 6. The sum of the sequence is
(number of terms) times (average of all the terms)
Since the sequence is arithmetic, the average of all the terms is the average of the first and last: (3+195)/2=99
The number of terms is
(last term minus first term), divided by 6, plus 1
The difference between the first and last terms, divided by the common difference, tells you the number of terms AFTER THE FIRST ONE; that's why you need to add 1 at the end.
195-3=192; 192/6=32; 32+1=33
So we have a sequence of 33 terms with an average of 99; the sum is
33(99)=33(100-1) = 3300-33 = 3267
ANSWER: 3267
|
|
|
