Question 1190567: Please help: the sum of the first two terms of a G.P is x.The sum of the last two is 1 if there are n term in all, calculate the common ratio
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
r = common ratio
Let's ignore the first two terms.
The last two terms of the geometric progression (GP), aka geometric sequence, sum to 1.
a = second to last term
ar = last term
a+ar = 1
ar = 1-a
r = (1-a)/a
If we had
a = 0.2
for instance, then it would mean,
r = (1-a)/a = (1-0.2)/0.2 = 0.8/0.2 = 4
ar = 0.2*4 = 0.8
a+ar = 0.2 + 0.8 = 1
Or we could have
a = 0.4
for instance, then it would mean
r = (1-a)/a = (1-0.4)/0.4 = 0.6/0.4 = 1.5
ar = 0.4*1.5 = 0.6
a+ar = 0.4 + 0.6 = 1
As you can see, these are two examples of having two terms of a geometric sequence add to 1.
It turns out there are infinitely many ways to do this.
It doesn't matter what those two original first terms sum to (ie. it doesn't matter what x is)
The problem is effectively the same as asking "the sum of the first two terms of a GP is 1. What is the common ratio?"
In short, there are infinitely many possible solutions here. There isn't enough info to answer this current question.
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
Please help: the sum of the first two terms of a G.P is x.The sum of the last two is 1.
if there are n term in all, calculate the common ratio
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let the GP be a, ar, ar^2, . . . , ar^(n-1).
The first term is "a", the common ratio is "r"; the number of terms is "n".
We are given
(a) the value of n; (the number of terms);
(b) a + ar = x; (the sum of the 1st and the 2nd terms, x)
(c) ar^(n-2) + ar^(n-1) = 1. (the sum of the two last terms, 1).
From (a), we have
a*(1+r) = x. (1)
From (b), we have
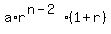 = 1. (2)
Now divide equation (2) by equation (1). You will get, after canceling common factors
 =  .
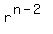It implies
r = 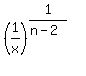 =  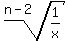=  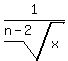. ANSWER
Any of the equivalent forms in the line above is the answer.
So, the value of the common ratio "r" is   by the input data x and n.
Solved.
===========
As a conclusion
The problem is posed correctly. It has (it admits) a unique solution.
Tutor @math_tutor2020 treated the problem incorrectly. He missed part of input data.
Therefore, his solution is incorrect.
His diagnosis
"there are infinitely many possible solutions here.
There isn't enough info to answer this current question."
is incorrect.
The problem is posed correctly, and I gave a complete solution/analysis.
|
|
|
