Question 1190223: a besieged fortress is held by 5700 men who have provisions for 66 days. of the garrison loses 20 men each day, for how many days will be provisions last?
Found 3 solutions by ikleyn, Edwin McCravy, Solver92311:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a besieged fortress is held by 5700 men who have provisions for 66 days.
of the garrison loses 20 men each day, for how many days will be provisions last?
~~~~~~~~~~~~~~
There are 5700*66 portions of provision in the storage.
In the 1st day, 5700 portions are consumed.
In the 2nd day, 5700-20 = 5680 portions are consumed.
In the 3nd day, 5680-20 = 5660 portions are consumed.
. . . and so on . . .
The problem wants you find the sum of the first n terms of this arithmetic progression
 = =  and the number n in such a way that
and the number n in such a way that  = 5700*66, under an additional condition = 5700*66, under an additional condition  >= 0.
The first term of this AP is 5700; the common difference is -20, so the sum of the first n terms is >= 0.
The first term of this AP is 5700; the common difference is -20, so the sum of the first n terms is
 = = 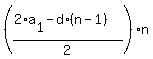 = = 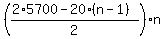 = = 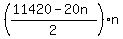 .
So we write this equation .
So we write this equation
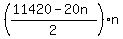 = 5700*66
Simplify
20n^2 - 11420n + 11400*66 = 0
n^2 - 571 + 5700*66 = 0.
Next, apply the quadratic formula. You will get = 5700*66
Simplify
20n^2 - 11420n + 11400*66 = 0
n^2 - 571 + 5700*66 = 0.
Next, apply the quadratic formula. You will get
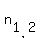 = = 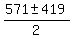 .
The value .
The value 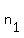 = = 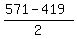 = 76 works: it satisfies = 76 works: it satisfies  = = 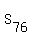 = 5700*66 and = 5700*66 and  >= 0.
The other value >= 0.
The other value 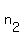 = = 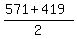 = 495 does not work: = 495 does not work: 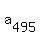 = 5700-20*495 = -4200 is negative.
So, the problem is just solved, and the ANSWER is 76 days. = 5700-20*495 = -4200 is negative.
So, the problem is just solved, and the ANSWER is 76 days.
Solved.
To check, I created an MS Excel spreadsheet, generated this AP there and calculated its sum.
The check confirmed that the answer is correct.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Answer by Solver92311(821)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If 5700 men have rations for 66 days, then there must be a total of 5700 times 66 or 376200 rations available.
On the first day, 5700 rations are used, but on the second day, 20 less are used, and on the third day, 20 less than that.
The total rations used is given by:

This is an arithmetic sequence where the first term is  , the common difference is , the common difference is  , there are , there are  terms (zero start), and the last term is terms (zero start), and the last term is  . .
Applying the formula for the sum of an arithmetic series:
(n\,+\,1))
Set this equal to the known total rations:
(n\,+\,1)\ =\ 376200)
And solve the quadratic for the smaller root
John

My calculator said it, I believe it, that settles it

From
I > Ø

|
|
|