.
As you see, and it is almost obvious, this sequence is an arithmetic progression.
The first term is 12 and the common difference is -5.
On the number line, the distance between the first term and the last term is
12 + 203 = 215.
The number of gaps between the terms in the number line is 
= 43.
Add 1 (one) to it, and you will get the number of terms of the progression: it is 43 + 1 = 44. ANSWER
It is the simplest way to solve this and hundreds other similar problems.
Your intuition and your common sense will dictate you what to do . . . without memorizing any formulas.
CHECK. To check, calculate the last term, using standard formula of an arithmetic progression
= 
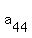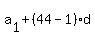= 12 - 43*5 = - 203. ! Correct !
Solved.
