.
Geometric mean of n terms  ,
,  , . . . ,
, . . . ,  is, BY THE DEFINITION, the root of degree n of the product of these terms
is, BY THE DEFINITION, the root of degree n of the product of these terms
 =
= 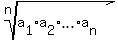 .
In this case, GM(2,4,8,16,32,64) =
.
In this case, GM(2,4,8,16,32,64) =  =
=  =
=  =
=  = 11.314 (rounded). ANSWER
= 11.314 (rounded). ANSWER
Solved.
--------------
On Geometric mean see this Wikipedia article
https://en.wikipedia.org/wiki/Geometric_mean