Question 1183761: Prove by math induction that
C(j,j) + C(j+1,j) + C(j+2,j) + ... + C(n+j,j) = C(n+j+1, j+1)
for all n >= 1 and arbitrary positive integer j.
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Prove by math induction that
C(j,j) + C(j+1,j) + C(j+2,j) + ... + C(n+j,j) = C(n+j+1, j+1)
for all n >= 1 and arbitrary positive integer j.
----------------
C(n,j) = n!/((n-j)!j!)
Base case, n=1:
LHS: C(j,j)+C(1+j,j) = 1 + (j+1)!/j! = j+2
RHS: C(1+j+1,j+1) = (j+2)!/(j+1)! = j+2
Base Case holds
Hypothesis: Assume
C(j,j) + C(j+1,j) + C(j+2,j) + ... + C(n+j,j) = C(n+j+1, j+1) (*)
is true for n=k.
Step case: let n=k+1:
...goal is to show LHS = RHS for n=k+1, making use of (*) when possible...
LHS:  + ... + + ... + 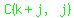 + C(k+j+1,j) + C(k+j+1,j)
where the green terms represent the n=k case and can be replaced (using (*)) by C(k+j+1, j+1):
LHS = C(k+j+1,j+1) + C(k+j+1,j)
= (k+j+1)!/(k!(j+1)!) + (k+j+1)!/((k+1)!j!)
...get this last expression over a common denominator...
= (k+1)(k+j+1)! / ((k+1)!(j+1)!) + (k+j+1)!(j+1) / ((k+1)!(j+1)!)
...factor out (k+j+1)! from numerator...
= (k+j+1)! ((k+1)+(j+1)) / ((k+1)!(j+1)!)
= (k+j+2)! / ((k+1)!(j+1)!) (1)
= C(k+j+2, j+1)
= RHS
This shows (*) holds for n=k+1, and the proof is complete.
-------
Alternate way to show LHS = RHS...
RHS: C((k+1)+j+1, j+1) = (k+j+2)!/((k+1)!(j+1)!) ( = (1) )
|
|
|