SOLUTION: Does the series (1/√(n^2+1^2) + 2/√(n^2+2^2) +...+(n-1)/√(n^2+(n-1)^2)+ n/√(n^2+n^2))/n converge as n goes to infinity? If it does, what is the sum?

Algebra ->  Sequences-and-series -> SOLUTION: Does the series (1/√(n^2+1^2) + 2/√(n^2+2^2) +...+(n-1)/√(n^2+(n-1)^2)+ n/√(n^2+n^2))/n converge as n goes to infinity? If it does, what is the sum?      Log On


   

Question 1183560: Does the series
(1/√(n^2+1^2) + 2/√(n^2+2^2) +...+(n-1)/√(n^2+(n-1)^2)+ n/√(n^2+n^2))/n
converge as n goes to infinity? If it does, what is the sum?
Found 2 solutions by ikleyn, robertb:
Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
Does the series
(1/√(n^2+1^2) + 2/√(n^2+2^2) +...+(n-1)/√(n^2+(n-1)^2)+ n/√(n^2+n^2))/n
converge as n goes to infinity? If it does, what is the sum?
~~~~~~~~~~~~~~~~~~~


            This problem is not for beginning Calculus students.
            It is for mature/advanced Calculus students.
            Therefore, I will give my solution without going into details,  assuming that the reader has an adequate level. 


The sum is

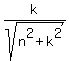    S%5Bn%5D = %281%2Fn%29%2Asum%28k%2Fsqrt%28n%5E2%2Bk%5E2%29%2C+k=1%2Cn%29.      (1)


Each term under the sum symbol can be estimated this way


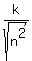    k%2Fsqrt%28n%5E2%2Bk%5E2%29 <= k%2Fsqrt%28n%5E2%29 = k%2Fn   from the top,                   (2)

and

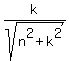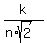    k%2Fsqrt%28n%5E2%2Bk%5E2%29 >= k%2Fsqrt%28n%5E2%2Bn%5E2%29 = k%2F%28n%2Asqrt%282%29%29  from the bottom,       (3)

or  

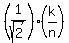    %281%2Fsqrt%282%29%29%2A%28k%2Fn%29 <= k%2Fsqrt%28n%5E2%2Bn%5E2%29 <= k%2Fn.      (4)



It gives, in turn, the following estimations for the entire sums  S%5Bn%5D


    %281%2Fsqrt%282%29%29%2A%281%2Fn%29%2Asum%28k%2Fn%2Ck=1%2Cn%29 <= S%5Bn%5D <= %281%2Fn%29%2Asum%28k%2Fn%2Ck=1%2Cn%29.      (5)


Next, each sum  sum%28%28k%2Fn%29%2Ck=1%2Cn%29  contains the sum of arithmetic progression  1 + 2 + 3 + . . . + n = %28n%2A%28n%2B1%29%29%2F2,

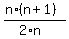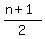therefore,   sum%28%28k%2Fn%29%2Ck=1%2Cn%29 = %28n%2A%28n%2B1%29%29%2F%282%2An%29 = %28n%2B1%29%2F2.


From this point, estimations (5) can be re-written


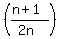    %281%2Fsqrt%282%29%29%2A%281%2F2%29 <= S%5Bn%5D <= %28%28n%2B1%29%2F%282n%29%29.      (6)


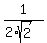Thus the terms  S%5Bn%5D  are asymptotically between  1%2F%282%2Asqrt%282%29%29  and  1%2F2.



        The sequence  S%5Bn%5D  is, actually,  monotonically DECREASING  sequence.



From the first glance, it seems to be unexpected statement, but it is true and it can be strictly established formally.

Therefore, of the two estimations (6) from the top and from the bottom, the only BOTTOM estimation makes sense for us now.


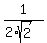So, we have the monotonically decreasing sequence  S%5Bn%5D  limited by the value  1%2F%282%2Asqrt%282%29%29  from the bottom --- THEREFORE,

     +--------------------------------------------+
     |   the sequence  S%5Bn%5D  is converged.         |
     +--------------------------------------------+



Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
lim%28n-%3Einfinity%2C+%281%2Fn%29%2Asum%28k%2Fsqrt%28n%5E2%2Bk%5E2%29%2C+k=1%2Cn%29%29
=

=
The term inside the summation eerily seems like the area of a rectangle whose width is 1%2Fn, and whose height is %28k%2Fn%29%2Fsqrt%281%2B%28k%2Fn%29%29%5E2.
As such, this looks like the equipartition of the interval [0,1] in the construction of the upper Riemann sums for the function f%28x%29+=+x%2Fsqrt%281%2Bx%5E2%29. Hence,
.
The integral is easily evaluated as sqrt%282%29-1. Therefore, the infinite series converges and the sum is sqrt%282%29+-+1, approximately 0.41421 to 5 d.p.