Question 1178154: Consider each given sequence start. i) Classify each as arithmetic, geometric, and/or none of these. ii) Find the 28th term. iii) Find the sum of the first 7 terms, call it S7 .
88,83, 78, 73,
Found 2 solutions by mananth, MathLover1:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
88,83, 78, 73,
common difference between consecutive terms is -5
first term a = 88
tn = a + (n-1)*d
t28 = 88+(87)*-5
t28 = -347
Sum of terms = Sn = n/2(2a+(n-1)d)
S7 = (7/2)(2*88+ 6*-5)
S7 =(7/2) * 146
S7 =511
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 , , , , 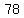 , ,  ,... ,...
1st term 
2nd term 
3rd term 
=> common difference is 
i) Classify each as arithmetic, geometric, and/or none of these.
=> common difference is  , so you have an arithmetic sequence , so you have an arithmetic sequence
 th term formula will be: th term formula will be:


ii) Find the 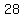 th term. th term.




iii) Find the sum of the first  terms, call it terms, call it  . .
first find  th, th,  th, and th, and  th term th term



 , , , , 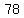 , ,  , ,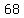 , , , ,
the sum is 
|
|
|