SOLUTION: Do the following sequences converge or diverge? If they converge, state the limit. a. {{{ (5n/(2n+1)) }}} b. {{{ ((n^3+1)/(2n+1)) }}} c. {{{ (3n^3/(4n^(5)+1)) }}}

 

There are certain rules apply when you have a polynomial numerator and a
polynomial denominator.

a.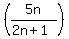 
This is convergent because the degree of the numerator is equal to the
degree of the denominator.


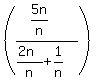
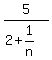And since  approaches 0, the sequence converges and the limit
is .  [That shows why but the rule goes that whenever the degree of
the numerator is equal to the degree of the denominator, the limit always
turns out to be fraction which which is the ratio of the two leading
coefficients.]

b.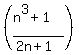 
2/3, 9/5, 4, 65/9, 126/11, ...  the rule goes that the sequence is divergent
whenever the degree of the numerator is greater than the degree of the
denominator.  That's because it eventually gets bigger than any number you
or anybody else can name.

c. 
3/5, 8/43, 81/973, 192/4097, 125/4167, ...
Converges to limit 0 whenever the degree of the numerator is less than the
degree of the denominator.   That's because it eventually gets smaller in
absolute value than any number you or anybody else can name.

Edwin