SOLUTION: 18 a Find 1 + 2 + . . . + 24. b Show that 1/n, 2/n + ... n/n = (n+1)/2 c Hence find the sum of the first 300 terms of 1/1 + 1/2 + 2/2 + 1/3 + 2/3 + 3/3 + 1/4 + 2/4 + 3/4 +4/

(a)  Find 1 + 2 + . . . + 24.

(b)  Show that 1/n, 2/n + ... n/n = (n+1)/2

(c)  Hence find the sum of the first 300 terms of
        1/1 + 1/2 + 2/2 + 1/3 + 2/3 + 3/3 + 1/4 + 2/4 + 3/4 +4/4 + ...

Well known fact is that the sum of the first n natural numbers

1 + 2 + 3 + . . . + n  is equal to  .     (1)


For the proof, see the lessons

    - Arithmetic progressions

    - The proofs of the formulas for arithmetic progressions 

in this site.



(a)  Therefore,  1 + 2 + 3 + . . . + 24 =  = 300.



(b)  From the formula (1),


          +  + . . .  +  =  = .



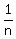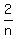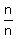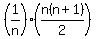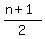(c)  Group the sum in this way


         Sum = (1/1) + (1/2 + 2/2) + (1/3 + 2/3 + 3/3) + (1/4 + 2/4 + 3/4 + 4/4) + . . .       (2)


     We have 300 terms/addends in all and the number of terms in k-th separate parentheses is k.


     Referring to the previous part (b) of this problem, we conclude that there are 24 groups in parentheses in the sum (2).


     Each particular group (k-th group) has the sum equal to 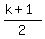, according to part (b) of the solution.


     In other words,


         Sum =  =  =  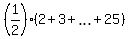=  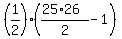=  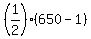=  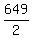= 324  = 324.5.    ANSWER