Question 1169187: The sum of the first and 4th term of a G.P is -1575 while the sum of the 3rd and 6th term is -25200. Find the first term, common ratio, and the sum of the 4th to 20th term inclusive.
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
a, ar, ar^2, ar^3, ar^4, ar^5, ar^6, ...
 The sum of the 1st and 4th terms is -1575
 The sum of the 3rd and 6th terms is -25200
Factor out the common term a^2 in the second equation.
The common ratio r is either 4 or -4.
Suppose r=4. Then the sum of the 1st and 4th terms is
That gives a non-integer value for the first term a.
So let's try r=-4.
The first term is a=25; the common ratio is a=-4.
The first few terms are
25, -100, 400, -1600, 6400, -25600, ....
To find the sum of the 4th through 20th terms, find the sum of the first 20 terms and subtract the sum of the first 3 terms.
The 20th term of the sequence is 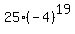 , which is about -6.87x10^12, so you will need a calculator that can handle large numbers if you need to get an exact answer. An excel spreadsheet is one option that will work nicely.
|
|
|
