Question 1167120: I am given the first three and the last term for this sequence. I need to know the number of terms for this?
1-k, 1+k, 1+3k..., 1+19k
Found 2 solutions by math_helper, ikleyn:
Answer by math_helper(2461)   (Show Source):
You can put this solution on YOUR website!
1: 1-k
2: 1+k (2k was added to term 1)
3: 1+3k (2k was added to term 2)
Now looking at this, you can say the n'th term will be (1-k) + 2(n-1)k
As a check, look at term 3 above, we can plug in n=3: (1-k) + 2(3-1)k = (1-k) + 4k = 1+3k
Setting 1+19k = (1-k)+2(n-1)k and re-writing:
1+19k = 1-3k+2nk
19k = -3k+2nk << subtracted 1 from both sides
19 = -3+2n << divided both sides by k
22 = 2n << added 3 to both sides
11 = n << divided both sides by 2
n = 11, and n=1 is the first term, so there are 11 terms in the sequence.
Answer by ikleyn(52790)  (Show Source):
You can put this solution on YOUR website! .
Number of terms is the same, as the number of terms in the sequence
-1, 1, 3, 5, . . . , 19.
Even if you know nothing about arithmetic progressions, and even if you are 2-nd grade student,
you can solve this problem and answer this question by writing all the terms of the sequence in a row and counting them.
But if you are a bit more advanced thinker, you may figure out that the number of gaps between 1 an 19 is
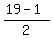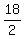 =  = 9;
Hence, the number of term in the sequence 1, 3, 5, . . . , 19 is 10;
Then joining the term {-1}, you get that the number under the problem's question is 10 + 1 = 11. ANSWER
|
|
|
