SOLUTION: For the arithmetic sequence with t7 = 0.6 and t12 = -0.4, find t20.

The distance between 0.6 and -0.4 in number line is 1 unit (0.6 - (-0.4) = 1).


There are 5 equal gaps between these points in number line, representing common difference of the arithmetic progression.

Hence, each gap has the length  1/5 = 0.2.

It means that the common difference of the AP is -0.2.   (It is negative, since the progression decreases).


Next, from    to 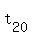 ,  there are 8 gaps in the number line, so the 20-th term is


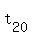     =  + 8*d = -0.4 + 8*(-0.2) = -0.4 - 1.6 = -2.0.    ANSWER