Question 1164382: 3, -6, 12, 4, 20, ?
Found 3 solutions by solver91311, ikleyn, greenestamps:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
16,000,000
or 200,000.
or - 8.
or -8.73.
or  . .
or 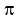 = 3.14... = 3.14...
or e = 2.718...
or 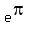 . .
or  . .
Or any other number.
Not a Math question.
G I B B E R I S H .
=============
I hear, from time to time, that some HR departments use such problems to estimate IQ of the employees
(or future employees).
I grab my head then . . .
How can these (. . . an omitted word . . .) estimate somebodies' IQ giving them mathematically incorrect questions (? ? ?)
Let me tell you one popular joke, which perfectly suits this situation.
"If a person is able to do his job, he does.
If a person is not able to do his job, he starts to teach.
If the person can not teach, he becomes a manager".
Yes, it is a joke, but this time I am about that managers from HR departments.
In this sense, I am very happy person, because NOBODY, NOWHERE and NEVER asked me such gibberish.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
One tutor responded saying the question is not a math problem, but it is instead gibberish.
In fact, her message is that there is no way to know what the next number is; ANY next number forms a valid sequence. So finding "THE" answer to ANY problem like this is a matter of getting in the mind of the author of the problem. And that is not math.
Another tutor responded with a solution using a logical pattern, so his solution is one good POSSIBLE solution.
But we can find other mathematically sound solutions -- showing that it is impossible to know the "right" answer.
Given a sequence of n numbers, we can always find a polynomial of degree (n-1) (or greater) that produces that sequence. So this sequence of 5 numbers can be produced by a polynomial of degree 4 -- a polynomial of the form
 . .
We could generate that polynomial by solving a system of equations that says
p(1) = 3
p(2) = -6
p(3) = 12
p(4) = 4
p(5) = 20
But since the problem only asks for the next term, we don't need to find that polynomial. We can use the method of finite differences to find the next term (or the next several, if we wanted to).
3 -6 12 4 20 given sequence
-9 18 -8 16 first differences
27 -26 24 second differences
-53 50 third differences
103 fourth differences
In a polynomial of degree 4, the fourth differences will be constant. (If you know some basic calculus, that is because the 4th derivative of a polynomial of degree 4 is a constant.)
To find the next number in the sequence, we can show that fourth difference one more time and then work back up the array of numbers.
3 -6 12 4 20 213
-9 18 -8 16 193
27 -26 24 177
-53 50 153
103 103
This shows that, if the sequence is produced by a polynomial of degree 4, the next number in the sequence is 213.
In playing with this problem, I found the polynomial that produces the given sequence, using matrices on a TI-83 calculator. That polynomial produces 213 for the next number in the sequence, agreeing with the result above.
That's very different from the answer the other tutor got using a different logical method.
Finding two very different answers by different methods that are both logical and valid is a good demonstration of the fact that it is not possible to find the "right" answer to any question like this.
|
|
|