SOLUTION: the sum of the first four terms of a linear sequence(A.P)is 26 and that of the next four terms is 74. Find the value of: (¡) the first term; (¡¡) the common difference.

Algebra ->  Sequences-and-series -> SOLUTION: the sum of the first four terms of a linear sequence(A.P)is 26 and that of the next four terms is 74. Find the value of: (¡) the first term; (¡¡) the common difference.      Log On


   

Question 1162919: the sum of the first four terms of a linear sequence(A.P)is 26 and that of
the next four terms is 74. Find the value of:
(¡) the first term;
(¡¡) the common difference.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
the sum of the first four terms of a linear sequence(A.P)is 26 and that of
the next four terms is 74. Find the value of:
(¡) the first term;
(¡¡) the common difference.
%221.%22a%5B1%5D%2B%28a%5B1%5D%2Bd%29%2B%28a%5B1%5D%2B2d%29%2B%28a%5B1%5D%2B3d%29=26

%222.%224a%5B1%5D%2B6d=26

%223.%222a%5B1%5D%2B3d=13


%224.%22%28a%5B1%5D%2B4d%29%2B%28a%5B1%5D%2B5d%29%2B%28a%5B1%5D%2B6d%29%2B%28a%5B1%5D%2B7d%29=74

%225.%224a%5B1%5D%2B22d=74

%225.%222a%5B1%5D%2B11d=37
From 3 and 6, we have

system%282a%5B1%5D%2B3d=13%2C+2a%5B1%5D%2B11d=37%29

Solve that system for first term a1 and common difference d.

Edwin

Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.

The sum of the first 4 terms is  a%5B1%5D + a%5B2%5D + a%5B3%5D + a%5B4%5D.


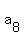The sum of the next 4 terms is  a%5B5%5D + a%5B6%5D + a%5B7%5D + a%5B8%5D.


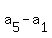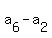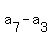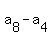Each difference  a%5B5%5D-a%5B1%5D,  a%5B6%5D-a%5B2%5D,  a%5B7%5D-a%5B3%5D  and  a%5B8%5D-a%5B4%5D  is equal to 4d,

where d is the common difference of the AP.



Therefore,  4*(4d) = 74 - 26,   or  16d = 48;  hence, d = 48/16 = 3.



Next,  26 = 4a + (1+2+3)d = 4a + 6*3 = 4a + 18,  which implies


       4a = 26 - 18 = 8.


Answer.  The first term of the AP is 8/4 = 2;  the common difference is 3.

Solved.

The goal of this problem is to teach you manipulate with AP terms quickly and informally.

It is a simple problem; so, the method of its solution should be adequately simple.

------------------

On arithmetic progressions, see the lessons
    - Arithmetic progressions
    - The proofs of the formulas for arithmetic progressions
    - Problems on arithmetic progressions
    - Word problems on arithmetic progressions
    - One characteristic property of arithmetic progressions
    - Solved problems on arithmetic progressions
    - Calculating partial sums of arithmetic progressions
    - Finding number of terms of an arithmetic progression
    - Advanced problems on arithmetic progressions
    - Problems on arithmetic progressions solved MENTALLY
in this site.

Also,  you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".


Save the link to this textbook together with its description

Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson

into your archive and use when it is needed.