SOLUTION: The first and the last term of an A.P are 21 and -47 respectively if the sum of the sequence is given is -234, calculate (I)the number of terms in the A.P (ii)the common difference

Algebra ->  Sequences-and-series -> SOLUTION: The first and the last term of an A.P are 21 and -47 respectively if the sum of the sequence is given is -234, calculate (I)the number of terms in the A.P (ii)the common difference      Log On


   

Question 1161640: The first and the last term of an A.P are 21 and -47 respectively if the sum of the sequence is given is -234, calculate (I)the number of terms in the A.P (ii)the common difference (iii)the sum of the first is term
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
first term, 21
last term, -47
sum of the sequence, -234
general term, 21+d(n-1) for d common difference which will be 'negative', and index of term n.

system%2821%2Bd%28n-1%29=-47%2C%28n%2F2%29%2821%2B%28-47%29%29=-234%29
Solve this system for n and for d.


The sum equation solved will give n=highlight%2818%29, or eighteen terms are in the sequence.

highlight%28d=-4%29, common difference is negative only because the sequence is decreasing.
General term 21-4%28n-1%29, another way to show.

Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.

To find the number of terms, first calculate the average of the two endpoint terms

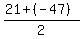    %2821+%2B+%28-47%29%29%2F2 = -13,

and then divide the given sum of the progression by this average

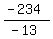    n = %28-234%29%2F%28-13%29 = 18.


So, the progression has 18 terms.



To find the common difference, first find the distance between the 1-st and the 18-th terms

    21 - (-47) = 21 + 47 = 68.


There are 17 equal gaps between the 1-st and 18-th terms; so each gap is 

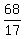    68%2F17 = 4,


and each gap is equal to the common difference taken with the opposite sign.


ANSWER.  (i)  n = 18;  (ii) d = -4.

Solved.

--------------

So, the problem can be solved MENTALLY, without using equation, if you know the properties of arithmetic progressions.

On arithmetic progressions, see the lessons
    - Arithmetic progressions
    - The proofs of the formulas for arithmetic progressions
    - Problems on arithmetic progressions
    - Word problems on arithmetic progressions
    - Chocolate bars and arithmetic progressions
    - One characteristic property of arithmetic progressions
    - Solved problems on arithmetic progressions
    - Calculating partial sums of arithmetic progressions
    - Advanced problems on arithmetic progressions
    - Interior angles of a polygon and Arithmetic progression
    - Problems on arithmetic progressions solved MENTALLY

Also,  you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".


Save the link to this textbook together with its description

Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson

into your archive and use when it is needed.