Question 1161390: A bouncing tennis ball rebounds each time to a height one-half the height of the previous bounce. if it is dropped from a height of 10m ,find:
a. The total distance it has travelled when it hits the ground for the 10th time,
b. The total distance it travels before coming to rest
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The ball hits the ground for the first time after dropping 10m,
and bounces up to 
In its first bounce round trip the tennis ball covers a distance of
 before hitting the ground for the second time.
As each bounce brings the ball up half the previous height,
each round trip adds to the distance travelled half as much distance as the one before.
The distances covered during each of those round trips form a geometric sequence, or geometric progression, or g.p. (depending on where you live).
If  is term number  on a g.p., and  is the ratio you have to multiply one term to get the next one,the formula for term number  is
With  and  , during round trip number ,
the ball travels  .
During round trip number  the ball travels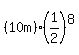 
The sun of the first terms of a g.p. is .
 , or  .
(we like the second version when  to avoid negative numbers).
After bounce round trips, the ball its the floor for the 10th time.
By then, it has travelled
 ,
accounting for a first downwards trip and up-and-down round trips.
Using the sum of first terms fpormula for  ,
we calculate it as
The sun of the first terms of a g.p. is .
, or
When , looking at ,
we realize that and the  }the denominator are constant,
but as increases 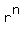 decreases , approaching  .
So when  for an infinite number of terms of a g.p.,
the sum is 
The total distance the bouncing tennis ball travels,
in its round trip bounces, before coming to rest is
Taking into account the first 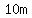 downwards trip before the first bounce, the total distance travelled is 
|
|
|
